Bài 1.3 trang 10 Toán 9 tập 1 Kết nối tri thức SGK

Đề Bài 1.3 trang 10 Toán 9:

Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) 2x – y = 3

b) 0x + 2y = –4

c) 3x + 0y = 5

Phân tích và Hướng dẫn giải:

Để giải bài toán này, các em cần thực hiện hai bước chính cho mỗi phương trình:

1. Viết nghiệm tổng quát:

   • Biến đổi phương trình về dạng $y=...$ hoặc $x=...$ để biểu diễn một ẩn qua ẩn còn lại.

   • Sau đó, viết nghiệm dưới dạng cặp số $(x;y)$ với một biến là tùy ý ($x\in \mathbb{R}$ hoặc $y\in \mathbb{R}$).

2. Biểu diễn hình học:

   • Nghiệm của một phương trình bậc nhất hai ẩn là tọa độ của các điểm trên một đường thẳng.

   • Để vẽ đường thẳng này, ta chỉ cần tìm tọa độ của hai điểm bất kỳ thuộc nó rồi nối lại. Giao điểm với trục hoành và trục tung thường là những điểm dễ tìm nhất.

Lời giải chi tiết:

a) 2x – y = 3 (1)

Viết (1) dưới dạng: y = 2x – 3

Ta có nghiệm tổng quát của (1) là: (x; 2x – 3) với x ∈ R tuỳ ý.

Biểu diễn hình học tất cả các nghiệm bằng cách vẽ đường thẳng d: y = 2x – 3

Vẽ d ta lấy hai điểm tuỳ ý thuộc d, chẳng hạn A(0; –3) và B(3/2;0)

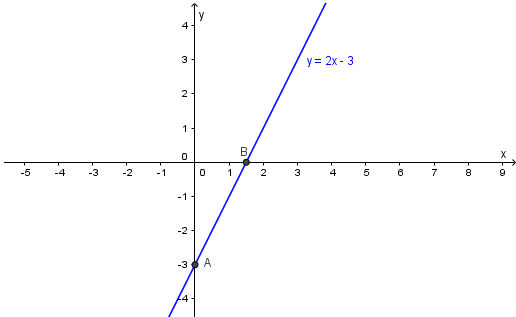
b) 0x + 2y = –4 (2)

Viết (2) dưới dạng: y = –2

Ta có nghiệm tổng quát của (2) là: (x; –2) với x ∈ R tuỳ ý.

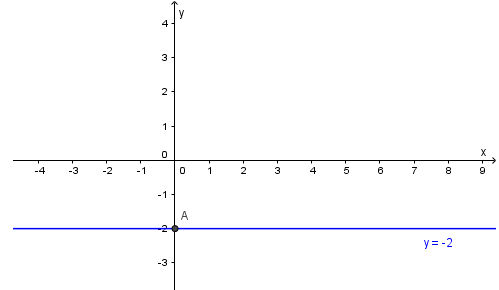
Biểu diễn hình học tất cả các nghiệm bằng cách vẽ đường thẳng d: y = –2

Vẽ d ta lấy hai điểm tuỳ ý thuộc d, chẳng hạn A(0; –2) và B(1; –2)

(y = –2 là đường thẳng song song trục hoành Ox)

c) 3x + 0y = 5 (3)

Viết (3) dưới dạng: x = 5/3

Ta có nghiệm tổng quát của (3) là: (5/3; y) với y ∈ R tuỳ ý.

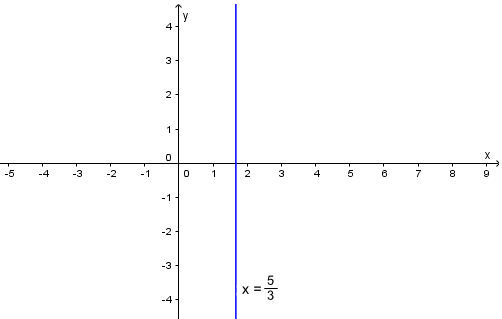
Biểu diễn hình học tất cả các nghiệm bằng cách vẽ đường thẳng d: x = 5/3

Vẽ d ta lấy hai điểm tuỳ ý thuộc d, chẳng hạn A(5/3; 0) và B(5/3; 1)

(x = 5/3 là đường thẳng song song trục tung Oy)