Bài 1 trang 25 Toán 11 tập 2 Cánh Diều
Bài tập số 1, trang 25 SGK Toán 11 Tập 2 (Cánh Diều), là bài toán cơ bản về thống kê, yêu cầu tính ba đại lượng đặc trưng quan trọng của mẫu số liệu ghép nhóm: Trung vị ($\text{Me}$), Tứ phân vị ($\text{Q}_1, \text{Q}_3$), và Mốt ($\text{M}_o$), dựa trên kết quả phỏng vấn về điểm số một mẫu áo sơ mi.
Bài 1 trang 25 Toán 11 tập 2 Cánh Diều:
Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm 100. Kết quả được trình bày trong Bảng 16.
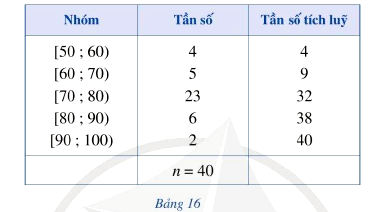
a) Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị:
A. 74. B. 75.
C. 76. D. 77.
b) Tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. Q1 ≈ 71; Q2 ≈ 76; Q3 ≈ 78.
B. Q1 ≈ 71; Q2 ≈ 75; Q3 ≈ 78.
C. Q1 ≈ 70; Q2 ≈ 76; Q3 ≈ 79.
D. Q1 ≈ 70; Q2 ≈ 75; Q3 ≈ 79.
c) Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. 73. B. 74.
C. 75. D. 76.
Phân Tích Dữ Liệu và Tần Số Tích Lũy
Tổng số phần tử $\mathbf{n = 40}$.
| Nhóm | Tần số (ni) | Tần số tích lũy (cfi) |
| $[50; 60)$ | 4 | 4 |
| $[60; 70)$ | 5 | 9 |
| $[70; 80)$ | 23 | 32 |
| $[80; 90)$ | 6 |
38 |
| $[80; 90)$ | 8 |
40 |
Giải bài 1 trang 25 Toán 11 tập 2 Cánh Diều:
a) Đáp án: B
Số phần tử của mẫu là: n = 40.
Ta có $\frac{n}{2}=\frac{40}{2}=20$
Mà 9 < 20 < 32 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.
Xét nhóm 3 là nhóm [70; 80) có r = 70, d = 10, n3 = 23 và nhóm 2 là nhóm [60; 70) có cf2 = 9.
Áp dụng công thức, ta có trung vị của mẫu số liệu là:
$M_e=r+\frac{\left ( \frac{n}{2}-cf_2 \right )}{n_3}.d$ $=70+\frac{20-9}{23}.10\approx 74,78$
Giá trị 74,78 gần nhất với giá trị 75.
b) Đáp án: D
⦁ Ta có: Q2 = Me ≈ 75 (điểm).
⦁ Ta có: $\frac{n}{4}=\frac{40}{4}=10$
Mà 9 < 10 < 32 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.
Xét nhóm 3 là nhóm [70; 80) có s = 70; h = 10; n3 = 23 và nhóm 2 là nhóm [60; 70) có cf2 = 9.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
$Q_1=s+\left ( \frac{\frac{n}{4}-cf_{p-1}}{n_p} \right ).h$ $=70+\frac{10-9}{23}.10\approx 70$
⦁ Ta có $ \frac{3n}{4}=\frac{3.40}{4}=30$
Mà 9 < 30 < 32 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 3 là nhóm [70; 80) có t = 70; l = 10; n3 = 23 và nhóm 2 là nhóm [60; 70) có cf2 = 9.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
$Q_3=t+\left ( \frac{\frac{3n}{4}-cf_{q-1}}{n_q} \right ).l$ $=70+\frac{30-9}{23}.10\approx 79$
Vậy Q1 ≈ 70; Q2 ≈ 75; Q3 ≈ 79.
c) Đáp án: C
Nhóm 3 là nhóm [70; 80) có tần số lớn nhất với u = 70, g = 10, n3 = 23 và nhóm 2 có tần số n2 = 5, nhóm 4 có tần số n4 = 6.
Áp dụng công thức, ta có mốt của mẫu số liệu là:
$M_o=u+\left (\frac{n_i-n_{i-1}}{2n_1-n_{i-1}-n_{i+1}} \right ).g$ $=70+\left (\frac{23-5}{2.23-5-6} \right ).10\approx 75$(điểm)
Bài toán đã được giải quyết bằng cách áp dụng các công thức nội suy cho mẫu số liệu ghép nhóm. Nhóm $\mathbf{[70; 80)}$ là nhóm chứa tất cả ba đại lượng Trung vị, Tứ phân vị thứ nhất và thứ ba, và Mốt, do tần số của nhóm này chiếm ưu thế ($n=23$). Các kết quả làm tròn đến hàng đơn vị là: Trung vị ($\text{Me}$) $\approx 75$, Tứ phân vị thứ nhất ($\text{Q}_1$) $\approx 70$, Tứ phân vị thứ ba ($\text{Q}_3$) $\approx 79$, và Mốt ($\text{M}_o$) $\approx 75$.
• Xem thêm:
Đánh giá & nhận xét
-
 Bài 7 trang 47 Toán 11 tập 2 Cánh Diều
Bài 7 trang 47 Toán 11 tập 2 Cánh Diều
-
 Bài 6 trang 47 Toán 11 tập 2 Cánh Diều
Bài 6 trang 47 Toán 11 tập 2 Cánh Diều
-
 Bài 5 trang 47 Toán 11 tập 2 Cánh Diều
Bài 5 trang 47 Toán 11 tập 2 Cánh Diều
-
 Bài 4 trang 47 Toán 11 tập 2 Cánh Diều
Bài 4 trang 47 Toán 11 tập 2 Cánh Diều
-
 Bài 3 trang 47 Toán 11 tập 2 Cánh Diều
Bài 3 trang 47 Toán 11 tập 2 Cánh Diều
-
 Bài 2 trang 47 Toán 11 tập 2 Cánh Diều
Bài 2 trang 47 Toán 11 tập 2 Cánh Diều
-
 Bài 1 trang 47 Toán 11 tập 2 Cánh Diều
Bài 1 trang 47 Toán 11 tập 2 Cánh Diều
-
 Bài 6 trang 33 Toán 11 tập 2 Cánh Diều
Bài 6 trang 33 Toán 11 tập 2 Cánh Diều
-
 Bài 5 trang 33 Toán 11 tập 2 Cánh Diều: So Sánh Lũy Thừa
Bài 5 trang 33 Toán 11 tập 2 Cánh Diều: So Sánh Lũy Thừa
-
 Bài 4 trang 33 Toán 11 tập 2 Cánh Diều: Viết Lũy Thừa Theo Thứ Tự Tăng Dần
Bài 4 trang 33 Toán 11 tập 2 Cánh Diều: Viết Lũy Thừa Theo Thứ Tự Tăng Dần
-
 Bài 3 trang 33 Toán 11 tập 2 Cánh Diều
Bài 3 trang 33 Toán 11 tập 2 Cánh Diều
-
 Bài 2 trang 33 Toán 11 tập 2 Cánh Diều
Bài 2 trang 33 Toán 11 tập 2 Cánh Diều
-
 Bài 1 trang 33 Toán 11 tập 2 Cánh Diều: Tính Biểu Thức Lũy Thừa
Bài 1 trang 33 Toán 11 tập 2 Cánh Diều: Tính Biểu Thức Lũy Thừa
-
 Bài 8 trang 26 Toán 11 tập 2 Cánh Diều
Bài 8 trang 26 Toán 11 tập 2 Cánh Diều
-
 Bài 7 trang 26 Toán 11 tập 2 Cánh Diều
Bài 7 trang 26 Toán 11 tập 2 Cánh Diều
-
 Bài 6 trang 26 Toán 11 tập 2 Cánh Diều
Bài 6 trang 26 Toán 11 tập 2 Cánh Diều
-
 Bài 5 trang 26 Toán 11 tập 2 Cánh Diều
Bài 5 trang 26 Toán 11 tập 2 Cánh Diều
-
 Bài 4 trang 26 Toán 11 tập 2 Cánh Diều
Bài 4 trang 26 Toán 11 tập 2 Cánh Diều
-
 Bài 3 trang 25 Toán 11 tập 2 Cánh Diều
Bài 3 trang 25 Toán 11 tập 2 Cánh Diều
-
 Bài 2 trang 25 Toán 11 tập 2 Cánh Diều
Bài 2 trang 25 Toán 11 tập 2 Cánh Diều
-
 Bài 6 trang 24 Toán 11 tập 2 Cánh Diều: Tính xác suất
Bài 6 trang 24 Toán 11 tập 2 Cánh Diều: Tính xác suất
-
 Bài 5 trang 24 Toán 11 tập 2 Cánh Diều
Bài 5 trang 24 Toán 11 tập 2 Cánh Diều
-
 Bài 4 trang 24 Toán 11 tập 2 Cánh Diều
Bài 4 trang 24 Toán 11 tập 2 Cánh Diều
-
 Bài 3 trang 24 Toán 11 tập 2 Cánh Diều
Bài 3 trang 24 Toán 11 tập 2 Cánh Diều
-
 Bài 2 trang 24 Toán 11 tập 2 Cánh Diều
Bài 2 trang 24 Toán 11 tập 2 Cánh Diều
-
 Bài 1 trang 24 Toán 11 tập 2 Cánh Diều
Bài 1 trang 24 Toán 11 tập 2 Cánh Diều
-
 Bài 1 trang 38 Toán 11 tập 2 Cánh Diều: Tính Lôgarit
Bài 1 trang 38 Toán 11 tập 2 Cánh Diều: Tính Lôgarit
-
 Bài 4 trang 55 Toán 11 tập 2 Cánh Diều
Bài 4 trang 55 Toán 11 tập 2 Cánh Diều
-
 Bài 3 trang 55 Toán 11 tập 2 Cánh Diều
Bài 3 trang 55 Toán 11 tập 2 Cánh Diều
-
 Bài 2 trang 55 Toán 11 tập 2 Cánh Diều
Bài 2 trang 55 Toán 11 tập 2 Cánh Diều
-
 Bài 1 trang 54 Toán 11 tập 2 Cánh Diều
Bài 1 trang 54 Toán 11 tập 2 Cánh Diều
-
 Bài 6 trang 38 Toán 11 tập 2 Cánh Diều
Bài 6 trang 38 Toán 11 tập 2 Cánh Diều
-
 Bài 5 trang 38 Toán 11 tập 2 Cánh Diều
Bài 5 trang 38 Toán 11 tập 2 Cánh Diều
-
 Bài 4 trang 38 Toán 11 tập 2 Cánh Diều
Bài 4 trang 38 Toán 11 tập 2 Cánh Diều
-
 Bài 3 trang 38 Toán 11 tập 2 Cánh Diều
Bài 3 trang 38 Toán 11 tập 2 Cánh Diều
-
 Bài 2 trang 38 Toán 11 tập 2 Cánh Diều
Bài 2 trang 38 Toán 11 tập 2 Cánh Diều
-
 Bài 3 trang 14 Toán 11 tập 2 Cánh Diều
Bài 3 trang 14 Toán 11 tập 2 Cánh Diều
-
 Bài 2 trang 14 Toán 11 tập 2 Cánh Diều
Bài 2 trang 14 Toán 11 tập 2 Cánh Diều
-
 Bài 1 trang 14 Toán 11 tập 2 Cánh Diều
Bài 1 trang 14 Toán 11 tập 2 Cánh Diều


















































