Hoán vị, chỉnh hợp, tổ hợp và bài tập áp dụng - Toán 11

Để các em hiểu rõ hơn về hoán vị, chỉnh hợp tổ hợp chúng ta cùng ôn lại kiến thức lý thuyết và vận dụng vào các bài tập cụ thể trong bài viết này nhé.

I. Tóm tắt lý thuyết hoán vị, chỉnh hợp và tổ hợp

1. Quy tắc đếm

a) Quy tắc cộng: Giả sử một công việc có thể được thực hiện theo phương án A hoặc phương án B . Có n cách thực hiện phương án A và m cách thực hiện phương án B. Khi đó công việc có thể thực hiện bởi n+m cách.

b) Quy tắc nhân: Giả sử một công việc nào đó bao gồm hai công đoạn  A và  B . Công đoạn  A có thể làm theo n  cách. Với mỗi cách thực hiện công đoạn A thì công đoạn B có thể làm theo m cách. Khi đó công việc có thể thực hiện theo n.m cách.

2. Hoán vị

+ Định nghĩa: Cho tập A gồm n phần tử (n≥1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập A được gọi là một hoán vị của n phần tử đó.

+ Số các hoán vị của một tập hợp có n phần tử là: P_n=n!=n(n-1)(n-2)...1.     

+ Chú ý: 0! = 1

* Ví dụ 1. Sắp xếp 5 người vào một băng ghế có 5 chỗ. Hỏi có bao nhiêu cách.

° Lời giải: Mỗi cách đổi chỗ 1 trong 5 người trên băng ghế là 1 hoán vị.

⇒ Vậy có P₅ = 5! = 120 cách sắp.

° Lời giải:

- Gọi A=a₁a₂a₃a₄a₅ với a₁≠0 và a₁, a₂, a₃, a₄, a₅ phân biệt là số cần lập.

+ Bước 1: chữ số a₁≠0 nên có 4 cách chọn a₁.

+ Bước 2: sắp 4 chữ số còn lại vào 4 vị trí có 4! = 24 cách.

⇒ Vậy có 4.24 = 96 số.

3. Chỉnh hợp

+ Định nghĩa: Cho một tập A gồm n phần tử (n≥1). Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.

+ Số các chỉnh hợp chập k của một tập hợp có n phần tử (1≤k≤n) là:

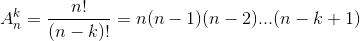
* Ví dụ 3. Sắp xếp 5 người vào một băng ghế có 7 chỗ. Hỏi có bao nhiêu cách.

° Lời giải: 

- Mỗi cách chọn ra 5 chỗ ngồi từ băng ghế để sắp 5 người vào và có hoán vị là một chỉnh hợp chập 5 của 7.

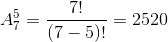
⇒ vậy có tổng cộng 2520 cách sắp.

* Ví dụ 4. Từ tập hợp X={0;1;2;3;4;5} có thể lập được mấy số tự nhiên có 4 chữ số khác nhau.

° Lời giải:

- Gọi A=a₁a₂a₃a₄với a₁≠0 và a₁, a₂, a₃, a₄, phân biệt là số cần lập

+ Bước 1: chữ số a1≠0 nên có 5 cách chọn a1.

+ Bước 2: chọn 3 trong 5 chữ số còn lại để sắp vào 3 vị trí chính là chỉnh hợp chập 3 của 5 phần tử .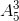

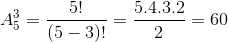
⇒ vậy ta có: 5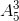=300 số

4. Tổ hợp

+ Định nghĩa: Cho tập hợp X gồm n phần tử phân biệt (n≥1). Mỗi cách chọn ra k (n ≥ k ≥ 1) phần tử của X được gọi là một tổ hợp chập k của n phần tử.

+ Số các tổ hợp chập k của n phần tử (1≤k≤n) là:

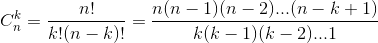
* Ví dụ 5. Có 10 cuốn sách toán khác nhau. Chọn ra 4 cuốn, hỏi có bao nhiêu cách.

° Lời giải: Mỗi cách chọn ra 4 trong 10 cuốn sách là một tổ hợp chập 4 của 10. vậy ta có:

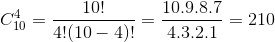
⇒ Vậy có 210 cách.

II. Bài tập áp dụng Hoán vị, chỉnh hợp và tổ hợp

* Bài tập 1. Trong một trường, khối 11 có 308 học sinh nam và 325 học sinh nữ. Hỏi có bao nhiêu cách chọn một học sinh khối 11 đi tham dự cuộc thi “huyền thoại đường Hồ Chí Minh trên biển” cấp huyện?

° Lời giải:

Trường hợp 1. Chọn 1 học sinh nam.  có 308 cách

Trường hợp 2. Chọn 1 học sinh nữ. Có 325 cách

Vậy, có 308 + 325 = 633 cách chọn một học sinh tham dự cuộc thi trên.

* Bài tập 2. Hỏi có bao nhiêu đa thức bậc ba.

P(x) =ax³+bx²+cx+d mà ác hệ số a, b, c, d thuộc tập {-3,-2,0,2,3}. Biết rằng.

a) Các hệ số tùy ý;

b) Các hệ số đều khác nhau.

° Lời giải:

a) Có 4 cách chọn hệ số a (vì a≠0). Có 5 cách chọn hệ số b, 5 cách chọn hệ số c, 4 cách chọn hệ số d. Vậy có. 4.5.5.5 =500 đa thức.

b) Có 4 cách chọn hệ số a (a≠0).

- Khi đã chọn a, có 4 cách chọn b.

- Khi đã chọn a và b, có 3 cách chọn c.

- Khi đã chọn a, b và c, có 2 cách chọn d.

Theo quy tắc nhân ta có. 4.4.3.2=96 đa thức.

* Bài tập 3. Một lớp trực tuần cần chọn 2 học sinh kéo cờ trong đó có 1 học sinh  nam, 1 học sinh  nữ. Biết lớp có 25 nữ và 15 nam. Hỏi có bao nhiêu cách chọn 2 học sinh kéo cờ nói trên.

° Lời giải:

Chọn học sinh nam ta có 15 cách chọn

Ứng với 1 học sinh  nam, chọn 1 học sinh nữ có 25 cách chọn

Vậy số cách chọn là 15. 25=375 cách.

* Bài tập 4. Từ các số 1, 2, 3, 4, 5, 6, 7 lập ra số tự nhiên có 4 chữ số đôi một khác nhau.

a) Hỏi lập được bao nhiêu số?

b) Có bao nhiêu số lẻ?

° Lời giải:

a) Số tự nhiên có bốn chữ số dạng là: abcd

Có 7 cách chọn a

Có 6 cách chọn b

Có 5 cách chọn c

Có 4 cách chọn d

Vậy có 7.6.5.4 = 840 số

b) Cách tính các số lẻ:

• Cách 1. Số tự nhiên lẻ có bốn chữ số dạng:abcd  

Vì số lẻ nên tận cùng là số lẻ nên d có 4 cách chọn.

Có 6 cách chọn a

Có 5 cách chọn b

Có 4 cách chọn c

Vậy có 4.6.5.4 = 480 số tự nhiên lẻ có bốn chữ số khác nhau

• Cách 2. Số tự nhiên lẻ có bốn chữ số khác nhau dạng: abc1 hoặc abc3 hoặc abc5 hoặc abc7

+ Xét số dạng abc1

chọn a có 6 cách

chọn b có 5 cách

chọn c có 4 cách

Vậy có 6.5.4 = 120 số lẻ dạng abc1

+ Tương tự các trường hợp còn lại. Vậy có 4.120 = 480 số lẻ có bốn chữ số được lập từ các số đã cho.

* Bài tập 5. Từ các số 0; 1; 2; 3; 4; 5; 6. lập ra số tự nhiên có 3 chữ số khác nhau.

a) Hỏi lập được bao nhiêu số.

b) Có bao nhiêu số chia hết cho 5.

° Lời giải:

a) Số tự nhiên có 3 chữ số dạng: abc

Có 6 cách chọn a vì a≠0.

Có 6 cách chọn b

Có 5 cách chọn c

Vậy có 6.6.5 = 180 số

b) Số tự nhiên có 3 chữ số và chia hết cho 5 dạng: ab0 hoặc ab5

+ Xét số dạng ab0

Có 6 cách chọn a và 5 cách chọn b. Vậy có 6.5 = 30 số

+ Xét số dạng ab5

Có 5 cách chọn a và 5 cách chọn b. Vậy có 5.5 = 25 số

⇒ Tổng số tự nhiên có 3 chữ số chia hết cho 5 là 30+25=55 số

* Bài tập 6. Trong giờ học môn Giáo dục quốc phòng, một tiểu đội học sinh gồm tám người được xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp?

° Lời giải:

Mỗi cách xếp 8 người thành một hàng dọc là một hoán vị của 8 phần tử.

Vậy số cách xếp 8 người thành hàng dọc là:  8!  = 8.7.6.5.4.3.2 = 40320 (cách xếp)

* Bài tập 7. Để tạo những tín hiệu, người ta dùng 5 lá cờ màu khác nhau cắm thành hàng ngang. Mỗi tín hiệu được xác định bởi số lá cờ và thứ tự sắp xếp. Hỏi có có thể tạo bao nhiêu tín hiệu nếu.

a) Cả 5 lá cờ đều được dùng;

b) Ít nhất một lá cờ được dùng.

° Lời giải:

a) Nếu dùng cả 5 lá cờ thì một tín hiệu chính là một hoán vị của 5 lá cờ.

Vậy có: 5! =120 tín hiệu được tạo ra.

b) Mỗi tín hiệu được tạo bởi k lá cờ là một chỉnh hợp chập k của 5 phần tử. Theo quy tắc cộng, có tất cả.

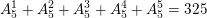 (tín hiệu).

* Bài tập 8. Từ một tổ gồm 6 bạn nam và 5 bạn nữ, chọn ngẫu nhiên 5 bạn xếp vào bàn đầu theo những thứ tự khác nhau sao cho trong cách xếp trên có đúng 3 bạn nam. Hỏi có bao nhiêu cách xếp.

° Lời giải:

Để xác định số cách xếp ta phải làm theo các công đoạn như sau.

1. Chọn 3 nam từ 6 nam. có C³₆ cách.
2. Chọn 2 nữ từ 5 nữ. có C²₅ cách.
3. Xếp 5 bạn đã chọn vào bàn đầu theo những thứ tự khác nhau. có 5! Cách.

⇒ Từ đó ta có số cách xếp là: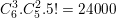 

* Bài tập 9. Một tổ chuyên môn gồm 7 thầy và 5 cô giáo, trong đó thầy P và cô Q là vợ chồng. Chọn ngẫu nhiên 5 người để lập hội đồng chấm thi vấn đáp. Có bao nhiêu cách lập sao cho hội đồng có 3 thầy, 2 cô và nhất thiết phải có thầy P hoặc cô Q nhưng không có cả hai.

° Lời giải:

♦ TH1. hội đồng gồm 3 thầy, 2 cô trong đó có thầy P nhưng không có cô Q. Khi đó ta cần chọn 2 trong 6 thầy còn lại (trừ thầy P)  rồi chọn 2 trong 4 cô (trừ cô Q)

      Có C²₆ . C²₄ = 90 (vì C²₆ = 15, C²₄ = 6)

♦ TH2. hội đồng gồm 3 thầy, 2 cô trong đó có cô Q nhưng không có thầy P. Khi đó ta cần chọn 3 trong 6 thầy còn lại (trừ thầy P) rồi chọn 1 trong 4 cô (trừ cô Q)

      Có C³₆ . C¹₄ = 80 (vì C³₆ = 20, C¹₄ = 4)

 Vậy, có C²₆ . C²₄ + C³₆ . C¹₄ = 90 + 80 = 170 cách lập hội đồng coi thi.       

>> Nhị thức Newton và bài tập áp dụng