Giải bài 9 trang 55 Toán 8 Tập 1 SGK Chân trời sáng tạo

Đề bài:

Tính diện tích xung quanh, diện tích toàn phần và thể tích của:

a) Hình chóp tam giác đều có chiều cao là 98,3 cm; tam giác đáy có độ dài cạnh là 40 cm và chiều cao là 34,6 cm; chiều cao mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là 99 cm.

b) Hình chóp tứ giác đều có độ dài cạnh đáy là 120 cm, chiều cao là 68,4 cm, chiều cao mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều là 91 cm.

Phân tích và Hướng dẫn giải:

Bài toán yêu cầu thực hiện các phép tính cho hai loại hình chóp đều: hình chóp tam giác đều và hình chóp tứ giác đều.

Để giải bài toán, các em cần nhớ các công thức sau:

• Diện tích xung quanh (S_xq​) = $\cdot (\text{chu vi đáy})\cdot (\text{trung đoạn})$.

• Diện tích đáy (S_đáy​) = diện tích của tam giác đều hoặc hình vuông đáy.

• Diện tích toàn phần (S_tp​) = S_xq​+S_đáy​.

• Thể tích ($V$) = ⋅S_đáy​⋅(chiều cao).

Ta sẽ áp dụng các công thức này cho từng hình chóp để tìm ra kết quả.

Lời giải chi tiết:

a) Ta có hình minh hoạ như sau:

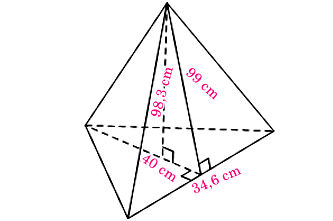
+ Diện tích xung quanh của hình chóp tam giác đều là:

+ Diện tích đáy của hình chóp tam giác đều là:

+ Diện tích toàn phần của hình chóp tam giác đều là:

 S_tp = S_xq + S_đáy = 5138,1 + 692 = 5830,1 (cm²).

+ Thể tích của hình chóp tam giác đều là:

b) Ta có hình minh hoạ như sau:

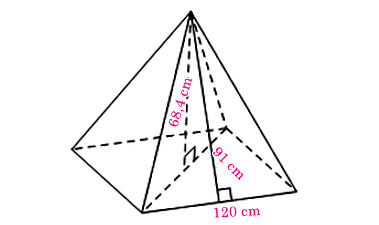
+ Diện tích xung quanh của hình chóp tứ giác đều là:

+ Diện tích đáy của hình chóp tứ giác đều là:

 S_đ = 120² = 14 400 (cm²).

+ Diện tích toàn phần của hình chóp tứ giác đều là:

 S_tp = S_xq + S_đ = 21 840 + 14 400 = 36 240 (cm²).

+ Thể tích của hình chóp tứ giác đều là: