Giải bài 4 trang 87 Toán 8 Tập 1 SGK Chân trời sáng tạo

Đề bài:

Cho tam giác ABC vuông tại A (AB < AC). Gọi D là trung điểm của BC. Vẽ DE // AB, vẽ DF // AC (E ∈ AC, F ∈ AB). Chứng minh rằng:

a) Tứ giác AEDF là hình chữ nhật.

b) Tứ giác BFED là hình bình hành.

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, chúng ta sẽ thực hiện theo các bước sau:

• Phần a: Chứng minh tứ giác $AEDF$ là hình chữ nhật.

  • Sử dụng dấu hiệu nhận biết hình chữ nhật dựa trên các góc vuông.

  • Sử dụng tính chất của đường thẳng song song để suy ra các góc vuông.

• Phần b: Chứng minh tứ giác $BFED$ là hình bình hành.

  • Có nhiều dấu hiệu nhận biết hình bình hành. Trong bài này, ta có thể chứng minh hai cạnh đối song song và bằng nhau.

  • Sử dụng kết quả từ phần a và tính chất đường trung tuyến trong tam giác vuông để chứng minh các cạnh bằng nhau.

Lời giải chi tiết:

Ta có hình minh họa như sau:

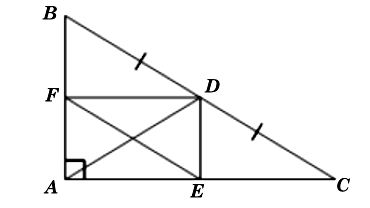
a) Tam giác ABC vuông tại A nên  hay AB ⊥ AC.

Do DE // AB và AB ⊥ AC nên DE ⊥ AC hay 

Do DF // AC và AB ⊥ AC nên DF ⊥ AB hay

Tứ giác AEDF có ;   và  nên là hình chữ nhật.

b) Do AEDF là hình chữ nhật nên AF = ED và AD = EF (tính chất hình chữ nhật).

• Xét ΔABC có AD là đường trung tuyến ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC, do đó:

Từ đó suy ra:

• Xét ΔBDF và ΔEFD có:

BD = EF (chứng minh trên);

DF là cạnh chung.

⇒ ΔBDF = ΔEFD (cạnh huyền – cạnh góc vuông).

⇒ FB = DE (hai cạnh tương ứng).

• Xét tứ giác BFED có FB = DE và FB // DE (do AB // DE)

⇒ BFED là hình bình hành.