Giải bài 3 trang 87 Toán 8 Tập 1 SGK Chân trời sáng tạo

Đề bài:

Cho tam giác ABC có đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K. 

a) Chứng minh tứ giác AHCE là hình chữ nhật.

b) Chứng minh HG = GK = KE.

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, chúng ta sẽ thực hiện theo các bước sau:

• Phần a: Chứng minh AHCE là hình chữ nhật.

  • Sử dụng dấu hiệu nhận biết của hình bình hành: tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

  • Sử dụng dấu hiệu nhận biết của hình chữ nhật: hình bình hành có một góc vuông.

• Phần b: Chứng minh HG = GK = KE.

  • Xác định vị trí của các điểm $G$ và $K$. Bạn sẽ thấy chúng là trọng tâm của các tam giác.

  • Áp dụng tính chất của trọng tâm: trọng tâm chia đường trung tuyến thành hai phần, một phần bằng 2/3​ độ dài đường trung tuyến và một phần bằng 1/3​ độ dài đường trung tuyến.

  • Sử dụng kết quả từ phần a và các tính chất đã biết để so sánh và chứng minh các đoạn thẳng bằng nhau.

Lời giải chi tiết:

Ta có hình minh họa như sau: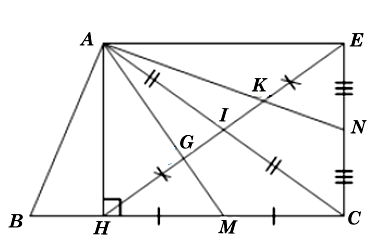

a) Do E là điểm đối xứng với H qua I nên I là trung điểm của HE.

Tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại trung điểm I của mỗi đường nên là hình bình hành.

Lại có  nên hình bình hành AHCE là hình chữ nhật.

b) Xét ΔAHC có AM, HI là hai đường trung tuyến cắt nhau tại G nên G là trọng tâm của ΔAHC.

Chứng minh tương tự đối với ΔAEC có K là trọng tâm của ΔAEC.

Ta có: 

Mà

Nên: 

Lại có:  và  nên

Hơn nữa: 

Vậy HG = GK = KE.