Giải bài 2 trang 71 Toán 8 Tập 1 SGK Chân trời sáng tạo

Đề bài:

Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang.

Phân tích và Hướng dẫn giải:

Đề bài cho tứ giác ABCD có AB = AD , và BD là tia phân giác của góc . Yêu cầu là chứng minh ABCD là hình thang.

Để chứng minh một tứ giác là hình thang, ta cần chứng tỏ nó có một cặp cạnh đối song song. Cụ thể, ta cần chứng minh AD // BC.

Ta sẽ thực hiện các bước sau:

1. Sử dụng tính chất tam giác cân: Từ AB = AD, ta suy ra tam giác ABD là tam giác cân tại A. Điều này dẫn đến hai góc đáy bằng nhau.

2. Sử dụng tính chất tia phân giác: Từ BD là tia phân giác của góc , ta suy ra hai góc nhỏ bằng nhau.

3. So sánh các góc: Từ hai bước trên, ta sẽ tìm được hai góc ở vị trí so le trong bằng nhau.

4. Kết luận: Dựa vào dấu hiệu nhận biết hai đường thẳng song song, ta sẽ kết luận AD // BC, từ đó suy ra ABCD là hình thang.

Lời giải chi tiết:

Ta có hình minh họa như sau:

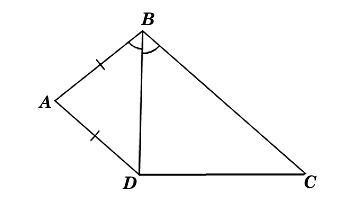
+ Xét DABD có AB = AD nên là tam giác cân tại A

 (tính chất tam giác cân)

+ Vì BD là tia phân giác của góc B nên

  (tính chất tia phân giác của một góc)

Mà hai góc này ở vị trí so le trong nên AD // BC.

+ Xét tứ giác ABCD có AD // BC nên là hình thang.

Vậy ABCD là hình thang.