Cách tính Góc giữa Đường thẳng và Mặt phẳng, Bài tập vận dụng - Toán hình 11

Vậy phương pháp tính góc giữa đường thẳng và mặt phẳng như thế nào? vận dụng vào bài tập ra sao? chúng ta cùng bắt đầu vào nội dung bài viết.

* Cách xác định góc giữa đường thẳng và mặt phẳng

- Để xác định được góc giữa đường thẳng a và mặt phẳng (α) ta thực hiện theo các bước sau:

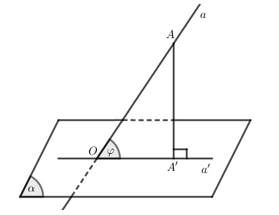
• Bước 1: Tìm giao điểm O của đường thẳng a và (α)

• Bước 2: Dựng hình chiếu A' của một điểm A ∈ a xuống (α)

• Bước 3: Góc ∠AOA' = φ chính là góc giữa đường thẳng a và (α)

> Lưu ý:

- Để dựng hình chiếu A' của điểm A trên (α) ta chọn một đường thẳng b ⊥ (α) khi đó AA' // b.

- Để tính góc φ ta sử dụng hệ thức lượng trong tam giác vuông OAA'.

* Cách xác định góc giữa đường thẳng và mặt phẳng qua ví dụ minh họa

* Ví dụ 1: Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Xác định góc giữa AC và mặt phẳng BCD.

* Lời giải:

- Ta có hình vẽ minh họa như sau:

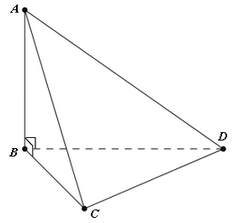- Theo giả thiết ta có: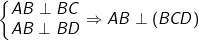 

- Từ đó, ta có góc giữa AC và mặt phẳng BCD là: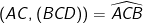 

* Ví dụ 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC).

* Lời giải:

 - Minh họa như hình vẽ: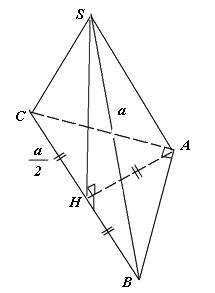

- Gọi H là trung điểm của BC, khi đó ta có:

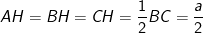
(H là trung điểm của BC, nên trung tuyến AH hạ từ đỉnh góc vuông A sẽ có độ dài bằng nửa cạnh huyền).

- Theo giả thiết H là hình chiếu vuông góc của S lên BC nên ta có:

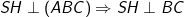  nên tan giác SHB vuông tại H.

- Áp dụng định lý pitago vào tam giác vuông SHB ta được: 

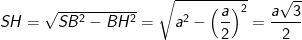
- Vậy góc giữa SA và (ABC) là SAH tức: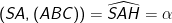 

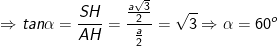
* Ví dụ 3: Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).

* Lời giải:

- Minh họa như hình sau: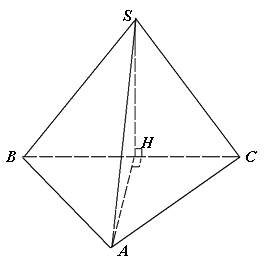- Do H là hình chiếu của S lên mặt phẳng (ABC) nên SH ⊥ (ABC)

Vậy AH là hình chiếu của SH lên mp(ABC)

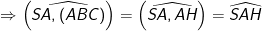
- Ta có: SH ⊥ (ABC) ⇒ SH ⊥ AH

 Mà: ΔABC = ΔSBC ⇒ SH = AH

⇒ Vậy ΔSAH vuông cân tại H ⇒ SAH = 45°

* Ví dụ 4: Cho hình thoi ABCD có tâm H, AC = 2a; BD = 2AC. Lấy điểm S không thuộc (ABCD) sao cho SH ⊥ (ABCD). Biết tan(SBH) = 1/2. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).

* Lời giải:

- Minh họa như hình sau: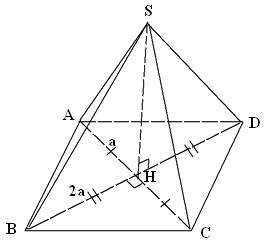

- Ta có: AC = 2a; BD = 2AC = 4a ⇒ HB = 2a.

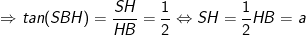
- Mặt khác, ta có: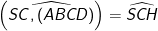 

 mà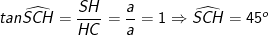 

Vậy số đo góc giữa đường thẳng SC và mặt phẳng (ABCD) là 45^o.

* Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = a√6. Hãy tính góc giữa SC và mp(ABCD).

* Lời giải:

- Minh họa như hình vẽ sau: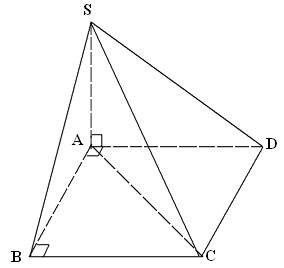

- Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên (ABCD)

⇒ Góc giữa giữa SC và mp(ABCD) bằng góc giữa SC và AC, tức là:

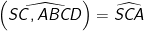
- Xét ΔSAC vuông tại A có:

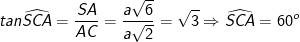
- Vậy góc giữa đường thẳng SC và mặt phẳng (ABCD) là 60^o.