Giải bài 43 trang 128 SGK Toán 9 tập 1
Hướng dẫn giải bài 43 trang 128 SGK Toán 9 Tập 1 cực hay, chi tiết dễ hiểu nhất để các em học sinh tham khảo
Bài 43 trang 128 SGK Toán 9 tập 1:
Cho hai đường tròn (O; R) và (O'; r) cắt nhau tại A và B (R > r). Gọi I là trung điểm của OO'. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt các đường tròn (O; R) và (O'; r) theo thứ tự C và D (khác A).
a) Chứng minh rằng AC = AD.
b) Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB.
Giải bài 43 trang 128 SGK Toán 9 tập 1:
Ta có hình minh hoạ như sau:
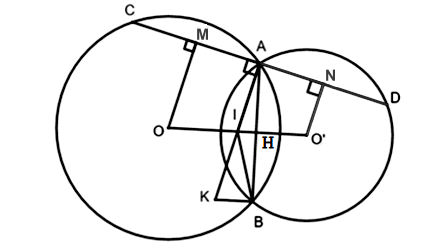
a) Chứng minh rằng AC = AD.
Vẽ OM ⊥ AC tại M, O’N ⊥ AD tại N
• Xét đường tròn (O), có:
OM ⊥ AC ⇒ MA = MC = AC/2 (định lý đường kính vuông góc với dây)
• Xét đường tròn (O'), có:
O'N ⊥ AD ⇒ NA = ND = AD/2 (định lý đường kính vuông góc với dây)
Mặt khác, ta có OM ⊥ CD, IA ⊥ CD, O'N ⊥ CD
⇒ OM // IA // O'N
Nên tứ giác OMNO' là hình thang.
• Xét hình thang OMNO', có:
IA // OM // O’N
IO = IO’ (I là trung điểm của OO’)
⇒ MA = NA (do đường thẳng song song với hai đáy của hình thang và đi qua trung điểm 1 cạnh bên thì đi qua trung điểm cạnh bên còn lại)
⇒ 2MA = 2NA ⇒ AC = AD.
b) Chứng minh rằng KB vuông góc với AB
Ta có (O) và (O’) cắt nhau tại A, B
Vì vậy, OO’ là đường trung trực của đoạn thẳng AB (tính chất đường nối tâm của hai đường tròn cắt nhau)
⇒ IA = IB (tính chất đường trung trực của đoạn thẳng)
Mặt khác IA = IK (vì K đối xứng với A qua I)
⇒ IA = IB = IK = AK/2
Xét ΔKBA, có BI là đường trung tuyến và BI = AK/2
Nên ΔKBA vuông tại B
⇒ KB ⊥ AB (đpcm).
Với nội dung bài 43 trang 128 SGK Toán 9 tập 1 cùng cách giải bài 43 trang 128 Toán 9 Tập 1 chi tiết, dễ hiểu. Hay Học Hỏi hy vọng giúp các em nắm vững phương pháp giải bài tập SGK Toán 9 tập 1. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt.
• Xem hướng dẫn giải bài tập SGK Toán 9 Tập 1 cùng chuyên mục
Đánh giá & nhận xét
-
 Bài 8.12 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.12 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.11 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.11 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.10 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.10 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.9 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.9 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.8 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.8 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.7 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.7 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.6 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.6 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.5 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.5 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.4 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.4 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.3 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.3 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.2 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.2 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 8.1 SGK Toán 9 tập 2 Kết nối tri thức
Bài 8.1 SGK Toán 9 tập 2 Kết nối tri thức
-
 Bài 4.27 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.27 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 18 trang 58 Toán 9 tập 1 Chân trời sáng tạo
Bài 18 trang 58 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 17 trang 58 Toán 9 tập 1 Chân trời sáng tạo
Bài 17 trang 58 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 16 trang 58 Toán 9 tập 1 Chân trời sáng tạo
Bài 16 trang 58 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 15 trang 58 Toán 9 tập 1 Chân trời sáng tạo
Bài 15 trang 58 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 14 trang 58 Toán 9 tập 1 Chân trời sáng tạo
Bài 14 trang 58 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 13 trang 58 Toán 9 tập 1 Chân trời sáng tạo
Bài 13 trang 58 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 12 trang 58 Toán 9 tập 1 Chân trời sáng tạo
Bài 12 trang 58 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 11 trang 58 Toán 9 tập 1 Chân trời sáng tạo
Bài 11 trang 58 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 10 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 10 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 9 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 9 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 8 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 8 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 7 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 7 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 6 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 6 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 5 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 5 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 4 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 4 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 3 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 3 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 2 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 2 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 1 trang 57 Toán 9 tập 1 Chân trời sáng tạo
Bài 1 trang 57 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 8 trang 56 Toán 9 tập 1 Chân trời sáng tạo
Bài 8 trang 56 Toán 9 tập 1 Chân trời sáng tạo
-
 Bài 7 trang 56 Toán 9 tập 1 Chân trời sáng tạo
Bài 7 trang 56 Toán 9 tập 1 Chân trời sáng tạo


















































