Giải bài 41 trang 128 SGK Toán 9 tập 1

Đề bài:

Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.

Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.

a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).

b) Tứ giác AEHF là hình gì? Vì sao?

c) Chứng minh đẳng thức AE.AB = AF.AC

d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).

e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, chúng ta sẽ lần lượt giải quyết từng phần một cách hệ thống:

• a) Vị trí tương đối: Xác định tâm và bán kính của các đường tròn để so sánh khoảng cách giữa các tâm với tổng hoặc hiệu bán kính.

• b) Tứ giác AEHF: Dựa vào các góc vuông đã cho trong đề bài để chứng minh AEHF là hình chữ nhật.

• c) Đẳng thức AE.AB = AF.AC: Áp dụng hệ thức lượng trong tam giác vuông để tìm mối liên hệ giữa các cạnh.

• d) Tiếp tuyến chung: Để chứng minh EF là tiếp tuyến chung của (I) và (K), ta cần chứng minh $EF\perp IE$ và $EF\perp KF$ tại các tiếp điểm E và F.

• e) Độ dài lớn nhất của EF: Tìm mối liên hệ giữa EF và một đại lượng khác có giá trị lớn nhất.

Lời giải chi tiết bài 41 trang 128 SGK Toán 9:

Ta có hình minh hoạ như sau:

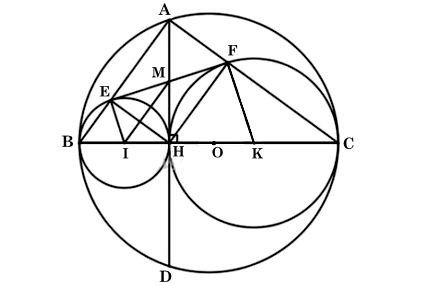
a) Vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).

Ta có:

OI = OB – IB nên (I) tiếp xúc trong với (O)

OK = OC – KC nên (K) tiếp xúc trong với (O)

IK = IH + KH nên (I) tiếp xúc ngoài với (K)

b) Tứ giác AEHF là hình gì? Vì sao?

Theo bài ra, ta có:

HE ⊥ AB tại E 

HK ⊥ AC tại F

Mà  (do A thuộc đường tròn đường kính BC)

Xét tứ giác AEHF có:

Nên tứ giác AEHF là hình chữ nhật.

c) Chứng minh đẳng thức AE.AB = AF.AC

Xét ΔABH vuông tại H có HE là đường cao

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AH² = AE. AB  (*)

Xét ΔACH vuông tại H có HF là đường cao

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AH² = AF. AC (**)

Từ (*) và (**) suy ra: AE. AB = AF. AC (vì cùng bằng AH²)

d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).

Gọi M là giao điểm của AH và EF, ta có: ME = MF = MH = MA (do AEHF là hình chữ nhật)

Xét ΔMEI và ΔMHI có:

ME = MH

IE = IH (cùng bằng bán kính đường tròn (I))

MI chung

⇒ ΔMEI = ΔMHI (c-c-c)

Mà AD vuông góc với BC tại H nên: 

⇒ ME ⊥ EI tại E

Mà IE là bán kính đường tròn (I)

Do đó, ME hay EF là tiếp tuyến của đường tròn (I)

• Mặt khác: Xét ΔMFH có:

MF = MH (chứng minh trên)

⇒ ΔMFH cân tại M

 (hai góc ở đáy) (*)

• Xét ΔKFH có:

KF = KH (cùng bằng bán kính đường tròn (K))

⇒ ΔKFH cân tại K

 (hai góc ở đáy) (**)

Từ (*) và (**) ta có:

 (do AH ⊥ BC tại H)

⇒ MF ⊥ FK tại F

Mà KF là bán kính đường tròn (K) nên MF hay EF là tiếp tuyến của đường tròn (K)

Vậy EF là tiếp tuyến chung của hai đường tròn (I) và (K).

e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.

Ta có thể giải theo 1 trong 2 cách sau:

* Cách giải 1:

Vì AEHF là hình chữ nhật nên ta có: EF = AH

Mà dây cung luôn nhỏ hơn hoặc bằng đường kính nên nửa dây cung luôn nhỏ hơn hoặc bằng bán kính nên ta có: AH ≤ AO.

Do đó, EF ≤ AO = R (với  R là bán kính của đường tròn (O) luôn không đổi)

Dấu bằng xảy ra khi H trùng với O

Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.

* Cách giải 2:

Ta có: EF = AH = AD/2

Nên EF lớn nhất khi AD lớn nhất.

Khi đó, dây AD là đường kính.

Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.