Lý Thuyết Toán 9 Bài 1: Phương Trình và Hệ Phương Trình Bậc Nhất Hai Ẩn (Kết Nối Tri Thức)

1. Phương Trình Bậc Nhất Hai Ẩn

• Khái niệm: Phương trình bậc nhất hai ẩn x và y là hệ thức có dạng ax + by = (1), trong đó a, b, c là các số đã biết và  hoặc .

• Nghiệm của phương trình: Nếu tại  và  ta có  là một khẳng định đúng thì cặp số  được gọi là một nghiệm của phương trình (1).

• Lưu ý: Một phương trình bậc nhất hai ẩn có vô số nghiệm.

Ví dụ 1: Nhận diện phương trình

• Các phương trình  là các phương trình bậc nhất hai ẩn x, y.

• Phương trình  không phải là phương trình bậc nhất hai ẩn vì cả hai hệ số của x và y đều bằng 0.

Ví dụ 2: Kiểm tra nghiệm

Trong các cặp số sau, cặp số nào là nghiệm của phương trình  a) (1; 2) b) (-1; -2) c) (3; 0)

• Hướng dẫn giải:

  • Thay x = 1 và y = 2, ta có: . Vậy (1; 2) không là nghiệm.

  • Thay x = -1 và y = -2, ta có: . Vậy (-1; -2) là một nghiệm.

  • Thay x = 3 và y = 0, ta có:  Vậy (3; 0) là một nghiệm.

• Nhận xét về biểu diễn hình học: Tập hợp tất cả các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn ax + by = c là một đường thẳng.

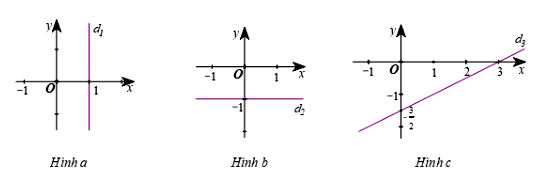
Ví dụ 3: Biểu diễn hình học các nghiệm

• a) x + 0y = 1: Ta viết gọn thành x = 1. Phương trình có nghiệm là (1; y) với  tùy ý. Đây là đường thẳng song song với trục tung và cắt trục hoành tại điểm (1; 0).

• b) 0x + y = -1: Ta viết gọn thành y = -1. Phương trình có nghiệm là (x; -1) với  tùy ý. Đây là đường thẳng song song với trục hoành và cắt trục tung tại điểm (0; -1).

• c) x - 2y = 3: Ta viết phương trình dưới dạng . Mỗi cặp số  với  tùy ý, là một nghiệm của phương trình. Đây là đường thẳng có phương trình . Để vẽ, ta có thể tìm hai điểm bất kỳ, ví dụ  và (3; 0), rồi vẽ đường thẳng đi qua chúng.

2. Hệ Hai Phương Trình Bậc Nhất Hai Ẩn

• Khái niệm: Một cặp gồm hai phương trình bậc nhất hai ẩn ax + by = c và a'x + b'y = c' được gọi là một hệ hai phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng:

  

Ví dụ 4: Nhận diện hệ phương trình

• Hệ phương trình  không phải là hệ phương trình bậc nhất hai ẩn vì phương trình thứ hai không phải là phương trình bậc nhất hai ẩn.

• Nghiệm của hệ phương trình: Mỗi cặp số  được gọi là một nghiệm của hệ nếu nó đồng thời là nghiệm của cả hai phương trình.

  • Lưu ý: Mỗi nghiệm của hệ chính là một nghiệm chung của hai phương trình trong hệ.

  • Nhận xét: Cặp số  là nghiệm của hệ phương trình cũng có nghĩa là điểm có tọa độ  là giao điểm của hai đường thẳng biểu diễn hai phương trình.

Ví dụ 5: Kiểm tra nghiệm của hệ phương trình

Cho hệ phương trình bậc nhất hai ẩn: . Trong các cặp số sau, cặp số nào là nghiệm của hệ đã cho? a) (0; -20) b) 

• Hướng dẫn giải:

  • a) Với cặp số (0; -20):

    • Phương trình (1): . Đúng.

    • Phương trình (2): . Sai.

    • Cặp số (0; -20) không phải là nghiệm của hệ.

  • b) Với cặp số :

    • Phương trình (1): . Đúng.

    • Phương trình (2): . Đúng.

    • Cặp số  là nghiệm của cả hai phương trình.

• Kết luận: Cặp số  là nghiệm của hệ phương trình đã cho.