Giải bài 4.14 trang 83 Toán 11 tập 1 SGK Kết nối tri thức

Bài 4.14 trang 83 Toán 11 tập 1 Kết nối tri thức:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC.

a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD).

b) Chứng minh rằng d song song với BD.

Giải bài 4.14 trang 83 Toán 11 tập 1 Kết nối tri thức:

Ta có hình minh hoạ như sau: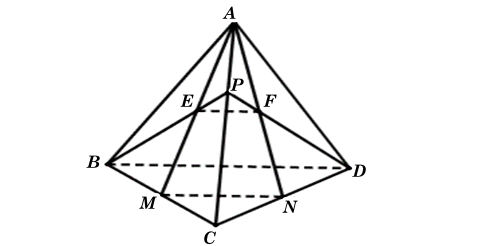

a) Trong ΔABC, gọi giao điểm của hai đường thẳng BP và AM là E.

Trong ΔACD, gọi giao điểm của hai đường thẳng DP và AN là F.

Vì E thuộc AM nên E thuộc mặt phẳng (AMN), vì F thuộc AN nên F thuộc mặt phẳng (AMN),

⇒ Đường thẳng EF nằm trong mặt phẳng (AMN).

Vì E thuộc BP nên E thuộc mặt phẳng (BPD), vì F thuộc DP nên F thuộc mặt phẳng (BPD),

⇒ Đường thẳng EF nằm trong mặt phẳng (BPD).

Vậy đường thẳng EF là giao tuyến của hai mặt phẳng (AMN) và (BPD) hay đường thẳng d cần tìm chính là đường thẳng EF.

b) Xét ΔBCD có M, N lần lượt là trung điểm của các cạnh BC, CD nên MN là đường trung bình của ΔBCD, do đó MN // BD.

Hai mặt phẳng (AMN) và (BPD) có chứa hai đường thẳng song song là MN và BD.

⇒ Giao tuyến d của hai mặt phẳng (AMN) và (BPD) song song với MN và BD.

Vậy d // BD.