Các dạng bài tập về quy tắc đếm (quy tắc cộng và quy tắc nhân) - Toán lớp 11

Vậy quy tắc cộng và quy tắc nhân được phát biểu như nào? chúng ta cùng tìm hiểu qua bài viết dưới đây, đồng thời giải các bài tập vận dụng hai quy tắc đếm này để dễ dàng ghi nhớ nội dung quy tắc.

I. Kiến thức cần nhớ về quy tắc cộng, quy tắc nhân

1. Quy tắc cộng

* Giả sử một công việc có thể tiến hành theo một trong k phương án A₁, A₂, . . . , A_k. Nếu:

 - Phương án A₁ có thể làm bằng n₁ cách.

 - Phương án A₂ có thể làm bằng n₂ cách.

 ...

 - Phương án A_k có thể làm bằng n_k cách.

 Khi đó, cả công việc có thể thực hiện theo 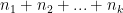 cách.

2. Quy tắc nhân

* Giả sử một công việc có thể tiến hành theo một trong k công đoạn A₁, A₂, . . . , A_k. Nếu:

 - Công đoạn A₁ có thể làm bằng n₁ cách.

 - Công đoạn A₂ có thể làm bằng n₂ cách.

 ...

 - Công đoạn A_k có thể làm bằng n_k cách.

 Khi đó, cả công việc có thể thực hiện theo 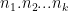 cách.

(Hiểu đơn giản: 1 công việc hoàn thành khi thực hiện k hành động liên tiếp)

II. Các dạng Bài tập quy tắc đếm

* Dạng 1: Đếm số phương án sử dụng các quy tắc đếm

* Phương pháp giải:

 ¤ Để sử dụng quy tắc cộng trong bài toán đếm, ta thực hiện theo các bước sau:

• Bước 1: Phân tích các phương án thành k nhóm độc lập với nhau: A₁, A₂, . . . , A_k.

• Bước 2: Nếu:

 - Phương án A₁ có thể làm bằng n₁ cách.

 - Phương án A₂ có thể làm bằng n₂ cách.

 ...

 - Phương án A_k có thể làm bằng n_k cách.

 • Bước 3: Khi đó, cả công việc có thể thực hiện theo 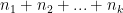 cách.

 ¤ Để sử dụng quy tắc nhân trong bài toán đếm, ta thực hiện theo các bước sau:

• Bước 1: Phân tích một hành động H thành k công việc nhỏ liên tiếp:  A₁, A₂, . . . , A_k. 

• Bước 2: Nếu:

 - A₁ có n₁ cách thực hiện khác nhau.

 - A₂ có n₂ cách thực hiện khác nhau.

 ...

 - A_k có n_k cách thực hiện khác nhau.

• Bước 3: Khi đó, ta có tất cả 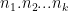 cách.

* Ví dụ 1 (Bài 3 trang 46 SGK Đại số 11): Dưới thành phố A, B, C, D được nối với nhau bởi các con đường như hình sau: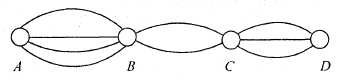Hỏi:

a) Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?

b) Có bao nhiêu cách đi từ A đến D rồi quay lại A?

° Lời giải:

a) Việc đi từ A đến D là công việc được hoàn thành bởi ba hành động liên tiếp:

+ Đi từ A đến B: Có 4 con đường.

+ Đi từ B đến C: Có 2 con đường.

+ Đi từ C đến D: Có 3 con đường

⇒ Theo quy tắc nhân: Có 4.3.2 = 24 con đường đi từ A đến D mà chỉ đi qua B và C 1 lần.

b) Có 24 cách đi từ A đến D thì cũng có 24 cách đi từ D đến A.

 Việc đi từ A đến D rồi lại quay lại A là công việc được hoàn thành bởi 2 hành động liên tiếp:

+ Đi từ A đến D: Có 24 cách .

+ Đi từ D về A : Có 24 cách

⇒ Theo quy tắc nhân: Có 24.24 = 576 cách đi.

* Ví dụ 2 (Bài 4 trang 46 SGK Đại số 11): Có ba kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?

° Lời giải:

 Việc chọn một chiếc đồng hồ cần thực hiện 2 hành động liên tiếp:

+ Chọn mặt đồng hồ: Có 3 cách chọn.

+ Chọn dây đồng hồ: Có 4 cách chọn.

⇒ Theo quy tắc nhân: Có 3.4 = 12 cách chọn đồng hồ.

* Ví dụ 3: Có 18 đội bóng tham gia thi đấu. Hỏi có bao nhiêu cách trao 3 loại huy chương vàng, bạc,
đồng cho 3 đội nhất, nhì, ba biết rằng mỗi đội có thể nhận nhiều nhất một huy chương và đội
nào cũng có khả năng đạt huy chương.

° Lời giải:

 Để lựa chọn trao 3 tấm huy chương cho 3 trong 18 đội ta thực hiện 3 hành động liên tiếp sau:

- Chọn 1 đội để trao huy chương vàng ta có: 18 lựa chọn

- Chọn 1 đội để trao huy chương bạc ta có: 17 lựa chọn (vì đã bớt đi đội được trao HCV)

- Chọn 1 đội để trao huy chương đồng ta có: 16 lựa (vì đã bớt đi đội được trao HCV, HCB)

⇒ Vậy theo quy tắc nhân: Có 18.17.16 = 4896 cách.

* Ví dụ 4: Trong một trường THPT, khối 11 có 280 học sinh nam và 325 học sinh nữ.

a) Nhà trường cần chọn một học sinh khối 11 để đi dự đại hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?

b) Nhà trường cần chọn hai học sinh khối 11 trong đó có một nam và một nữ đi dự trại hè của học sinh
thành phố. Hỏi nhà trường có bao nhiêu cách chọn?

° Lời giải:

a) Để chọn 1 học sinh đi dự đại hội của học sinh thành phố ta có thể chọn học sinh nam và học sinh nữ:

- Nếu chọn một học sinh nam ta có 280 cách.

- Nếu chọn một học sinh nữ ta có 325 cách.

→ Vậy theo qui tắc cộng, ta có 280 + 325 = 605 cách chọn. 

b)  Để lựa chọn 2 học sinh trong đó có một nam và một nữ đi dự trại hè của học sinh thành phố ta cần thực hiện 2 hành động liên tiếp sau:

- Chọn 1 học sinh Nam trong 280 học sinh: có 280 lựa chọn

- Chọn 1 học sinh Nữ trong 325 học sinh: có 325 lựa chọn

→ Vậy theo quy tắc nhân: Có 280.325 = 91000 cách.

* Dạng 2: Sử dụng các quy tắc đếm giải bài toán đếm các số hình thành từ tập A

* Phương pháp giải:

1. Sử dụng quy tắc nhân để thực hiện bài toán đếm số các số gồm k chữ số hình thành từ tập A, ta thực hiện các bước sau:

• Bước 1: Gọi số cần tìm có dạng 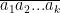 với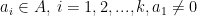 

• Bước 2: Đếm số cách chọn a_i, (không nhất thiết phải theo thứ tự) giả sử có n_i cách.

• Bước 3: Khi đó, ta có tất cả 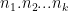 cách.

2. Sử dụng quy tắc cộng và quy tắc nhân để thực hiện bài toán đếm số các số gồm k chữ số hình thành từ tập A, ta thực hiện theo các bước sau:

• Bước 1: Chia các số cần tìm thành các tập con H₁, H₂, ... độc lập với nhau

• Bước 2: Sử dụng quy tắc nhân để đếm số phần từ của các tập H₁, H₂, ..., giả sử bằng k₁, k₂,...

• Bước 3: Khi đó, ta có tất cả 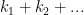 số.

* Ví dụ 1 (Bài 1 trang 46 SGK Đại số 11): Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm:

a) Một chữ số

b) Hai chữ số.

c) Hai chữ số kháu nhau?

° Lời giải:

a) Gọi số có 1 chữ số là a

- Chọn a có 4 cách chọn.

→ Vậy có 4 cách chọn số một chữ số.

b) Gọi số có 2 chữ số cần lập là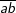 

- Hành động 1: chọn a ta có 4 cách chọn

- Hành động 2: chọn b ta có 4 cách chọn

→ Vậy theo quy tắc nhân ta có: 4.4 = 16 (cách lập)

c) Gọi số có 2 chữ số cần lập là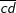 

- Hành động 1: Chọn c ta có 4 cách chọn

- Hành động 2: Chọn d ta có 3 cách chọn (vì d khác c).

→ Vậy theo quy tắc nhân ta có: 4.3 = 12 (cách lập).

* Ví dụ 2 (Bài 2 trang 46 SGK Đại số 11): Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?

° Lời giải:

* Phương án 1 (là trường hợp chỉ có 1 chữ số) : Số thỏa mãn có 1 chữ số: Có 6 số là: 1, 2, 3, 4, 5, 6.

 → Có 6 số có 1 chữ số thỏa điều kiện nhỏ hơn 100

* Phương án 2 (là trường hợp 2 có 2 chữ số): Số thỏa mãn có 2 chữ số:

- Hành động 1: Chọn chữ số hàng chục ta có 6 cách chọn

- Hành động 2: Chọn chữ số hàng đơn vị ta có 6 cách chọn

 → Theo quy tắc nhân: Có 6.6 = 36 số có 2 chữ số được tạo ra từ các số đã cho.

* Theo quy tắc cộng: Có 36 + 6 = 42 số tự nhiên bé hơn 100 được tạo ra từ các chữ số đã cho