Giải bài 1 trang 80 Toán 8 Tập 1 SGK Chân trời sáng tạo

Đề bài:

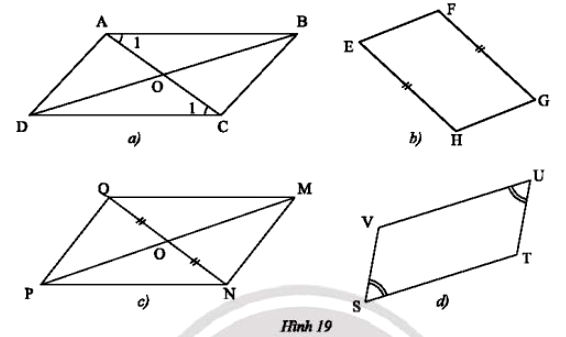
Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành hình bình hành?

Phân tích và Hướng dẫn giải:

Để giải quyết bài toán này, các em cần nhớ lại các dấu hiệu nhận biết hình bình hành:

1. Tứ giác có các cạnh đối song song.

2. Tứ giác có các cạnh đối bằng nhau.

3. Tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau.

4. Tứ giác có các góc đối bằng nhau.

5. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Ta sẽ phân tích từng hình vẽ để xem đã có những điều kiện nào và cần thêm điều kiện gì để thỏa mãn một trong các dấu hiệu trên.

Lời giải chi tiết:

• Hình 19a)

Ta có  và hai góc này ở vị trí so le trong nên AB // CD.

Để tứ giác ABCD là hình bình hành thì có hai trường hợp sau:

+) Trường hợp 1: Tứ giác ABCD có hai cặp cạnh đối song song. Do đó cần thêm điều kiện AD // BC.

+) Trường hợp 2: Tứ giác ABCD có cặp cạnh đối vừa song song, vừa bằng nhau. Do đó cần thêm điều kiện AB = CD.

• Hình 19b)

 Tứ giác EFGH đã có một cặp cạnh đối bằng nhau (EH = GF).

Để tứ giác EFGH là hình bình hành thì có hai trường hợp sau:

+) Trường hợp 1: Tứ giác EFGH có hai cặp cạnh đối bằng nhau. Do đó cần thêm điều kiện EF = GH.

+) Trường hợp 2: Tứ giác EFGH có cặp cạnh đối vừa song song, vừa bằng nhau. Do đó cần thêm điều kiện EH // GF.

• Hình 19c)

Ta có OQ = ON nên O là trung điểm của NQ.

Để tứ giác MNPQ là hình bình hành thì tứ giác MNPQ có hai đường chéo cắt nhau tại trung điểm của mỗi đường. Do đó cần thêm điều kiện O là trung điểm của MP.

• Hình 19d) 

Tứ giác STUV đã có một cặp góc đối bằng nhau

Để tứ giác STUV là hình bình hành thì tứ giác STUV có cac cặp góc đối bằng nhau. Do đó cần thêm điều kiện