Cách tìm điều kiện để biểu thức căn thức có nghĩa (xác định) và bài tập vận dụng - Toán 9 chuyên đề

15:38:4310/08/2021

Trong chương trình Toán lớp 9, việc tìm điều kiện xác định của biểu thức căn thức (hay còn gọi là cách tìm điều kiện để biểu thức chứa căn thức có nghĩa) là một trong những dạng toán cơ bản và quan trọng nhất. Dạng toán này không chỉ là một bài tập riêng biệt mà còn là bước đầu tiên không thể thiếu trong nhiều dạng toán khác như rút gọn biểu thức, giải phương trình chứa căn, hay tìm giá trị lớn nhất, nhỏ nhất.

Nắm vững cách tìm điều kiện xác định sẽ giúp bạn tránh được các lỗi sai cơ bản và làm nền tảng cho việc giải quyết các bài toán phức tạp hơn trong các kì thi quan trọng, đặc biệt là kì thi tuyển sinh vào lớp 10.

I. Cách tìm điều kiện để biểu thức căn thức có nghĩa

1. Phương pháp chung

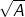• $\small \sqrt{A}$ có nghĩa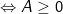 $\small \Leftrightarrow A\geq 0$

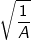• $\small \sqrt{\frac{1}{A}}$ có nghĩa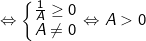 $\small \Leftrightarrow \left\{\begin{matrix} \frac{1}{A}\geq 0\\ A\neq 0 \end{matrix}\right.\Leftrightarrow A>0$

(vì biểu thức trong căn phải ≥ 0 và mẫu thức phải khác 0).

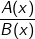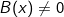
• $\small \frac{A(x)}{B(x)}$ có nghĩa khi $\small B(x)\neq 0$

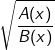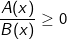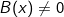
• $\small \sqrt{\frac{A(x)}{B(x)}}$ có nghĩa khi $\small \frac{A(x)}{B(x)}\geq 0$ và $\small B(x)\neq 0$

2. Lưu ý quan trọng

Nếu biểu thức chứa căn ở dưới mẫu, điều kiện của biểu thức trong căn phải là số dương (lớn hơn 0), không được bằng 0.
Nếu bài toán yêu cầu tìm tập xác định (TXĐ), sau khi tìm được điều kiện của $x$ , bạn cần biểu diễn kết quả dưới dạng tập hợp. Ví dụ: $x \geq 2$ sẽ được viết là $D = [2; + \infty)$ .

II. Bài tập Vận dụng: Tìm điều kiện xác định của căn thức

Bài tập 1: Tìm điều kiện của x để căn thức sau có nghĩa

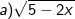
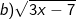
$\small a)\sqrt{5-2x}$ $\small b)\sqrt{3x-7}$

Lời giải:

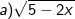
$\small a)\sqrt{5-2x}$

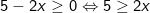
- Biểu thức này chỉ chứa căn bậc hai, nên biểu thức căn thức có nghĩa thì: $\small 5-2x\geq 0\Leftrightarrow 5\geq 2x$

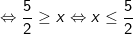
$\small \Leftrightarrow \frac{5}{2}\geq x\Leftrightarrow x\leq \frac{5}{2}$

Kết luận: Để căn thức có nghĩa thì x ≤ 5/2.

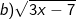
$\small b)\sqrt{3x-7}$

- Biểu thức này chỉ chứa căn bậc hai, nên biểu thức căn thức có nghĩa thì:

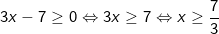
$\small 3x-7\geq 0\Leftrightarrow 3x\geq 7\Leftrightarrow x\geq \frac{7}{3}$

Kết luận: Để căn thức có nghĩa thì x ≥ 7/3.

Bài tập 2: Tìm điều kiện của x để biểu thức sau có nghĩa

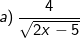
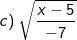
$\small a)\: \frac{4}{\sqrt{2x-5}}$ $\small b)\: \sqrt{\frac{9}{x-3}}$ $\small c)\: \sqrt{\frac{x-5}{-7}}$

Lời giải:

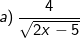
$\small a)\: \frac{4}{\sqrt{2x-5}}$

- Biểu thức này chứa căn bậc hai và đồng thời có phân thức ở mẫu, vì vậy để biểu thức có nghĩa thì:

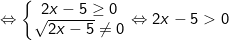
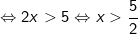
$\small \Leftrightarrow \left\{\begin{matrix} 2x-5\geq 0\\ \sqrt{2x-5}\neq 0 \end{matrix}\right.\Leftrightarrow 2x-5>0$ $\small \Leftrightarrow 2x>5\Leftrightarrow x>\frac{5}{2}$

Kết luận: Để biểu thức có nghĩa thì x > 5/2.

$\small b)\: \sqrt{\frac{9}{x-3}}$

- Biểu thức này chứa căn bậc hai và đồng thời có phân thức ở mẫu, vì vậy để biểu thức có nghĩa thì:

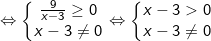
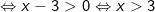
$\small \Leftrightarrow \left\{\begin{matrix} \frac{9}{x-3}\geq 0\\ x-3\neq 0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x-3>0\\ x-3\neq 0 \end{matrix}\right.$ $\small \Leftrightarrow x-3>0\Leftrightarrow x>3$

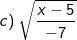
$\small c)\: \sqrt{\frac{x-5}{-7}}$

- Biểu thức này chứa căn bậc hai và mẫu thức đã là số khác 0 nên điều kiện để biểu thức có nghĩa là:

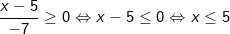
$\small \frac{x-5}{-7}\geq 0\Leftrightarrow x-5\leq 0\Leftrightarrow x\leq 5$

Bài tập 3: Tìm điều kiện của x để biểu thức sau có nghĩa

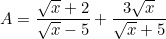
$\small A=\frac{\sqrt{x}+2}{\sqrt{x}-5}+\frac{3\sqrt{x}}{\sqrt{x}+5}$

Lời giải:

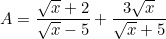
$\small A=\frac{\sqrt{x}+2}{\sqrt{x}-5}+\frac{3\sqrt{x}}{\sqrt{x}+5}$

Để biểu thức có nghĩa thì căn thức có nghĩa và phân thức có nghĩa, tức là các biểu thức trong căn bậc hai phải ≥ 0 và mẫu thức các phân tức phải ≠0. Nên ta có:

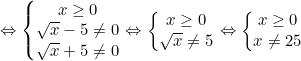
$\small \Leftrightarrow \left\{\begin{matrix} x\geq 0\\ \sqrt{x}-5\neq 0\\ \sqrt{x}+5\neq 0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x\geq 0\\ \sqrt{x}\neq 5 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x\geq 0\\ x\neq 25 \end{matrix}\right.$

Kết luận: Biểu thức có nghĩa khi x ≥ 0 và x ≠ 25

Bài tập 4: Tìm điều kiện của x để biểu thức sau có nghĩa

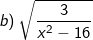
$\small a)\: \sqrt{x^2-6x+5}$ $\small b)\: \sqrt{\frac{3}{x^2-16}}$

Lời giải:

$\small a)\: \sqrt{x^2-6x+5}$

- Để biểu thức căn thức có nghĩa thì: x² - 6x + 5 ≥ 0

⇔ x² - 5x - x + 5 ≥ 0 ⇔ x(x - 5) - (x - 5) ≥ 0

⇔ (x - 5)(x - 1) ≥ 0

⇔ [(x - 5) ≥ 0 và (x - 1) ≥ 0] hoặc [(x - 5) ≤ 0 và (x - 1) ≤ 0]

⇔ [x ≥ 5 và x ≥ 1] hoặc [x ≤ 5 và x ≤ 1]

⇔ [x ≥ 5] hoặc [x ≤ 1]

Kết luận: biểu thức có nghĩa khi x≤1 hoặc x≥5.

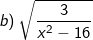
$\small b)\: \sqrt{\frac{3}{x^2-16}}$

- Để biểu thức có nghĩa thì biểu thức trong căn bậc hai không âm (tức lớn hơn bằng 0) và mẫu thức khác 0. Nên ta có:

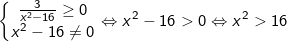
$\fn_cm \small \left\{\begin{matrix} \frac{3}{x^2-16}\geq 0\\ x^2-16\neq 0 \end{matrix}\right.\Leftrightarrow x^2-16>0\Leftrightarrow x^2> 16$

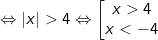
$\small \Leftrightarrow |x|>4 \Leftrightarrow \left \[\begin{matrix} x>4\\ x<-4 \end{matrix} \right.$

Kết luận: Biểu thức có nghĩa khi và chỉ khi x<-4 hoặc x>4.

Bài tập 5: Với giá trị nào của x thì biểu thức sau có nghĩa:

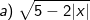
$\small a)\: \sqrt{5-2|x|}$

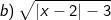
$\small b)\: \sqrt{|x-2|-3}$

Lời giải:

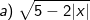
$\small a)\: \sqrt{5-2|x|}$

- Để biểu thức có nghĩa thì: 5 - 2|x| ≥ 0

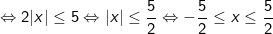
$\small \Leftrightarrow 2|x|\leq 5\Leftrightarrow |x|\leq \frac{5}{2} \Leftrightarrow -\frac{5}{2}\leq x\leq \frac{5}{2}$

Vậy biểu thức có nghĩa khi và chỉ khi 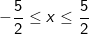$\small -\frac{5}{2}\leq x\leq \frac{5}{2}$

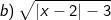
$\small b)\: \sqrt{|x-2|-3}$

- Để biểu thức có nghĩa thì: |x - 2| - 3 ≥ 0

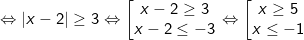
$\small \Leftrightarrow |x-2|\geq 3\Leftrightarrow \left \[\begin{matrix} x-2\geq 3\\ x-2\leq -3 \end{matrix} \right. \Leftrightarrow \left \[\begin{matrix} x\geq 5\\ x\leq -1 \end{matrix} \right.$

Vậy biểu thức có nghĩa khi và chỉ khi x≤-1 hoặc x≥5.

Bài tập 6: Với giá trị nào của x thì biểu thức sau có nghĩa:

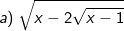
$\small a)\: \sqrt{x-2\sqrt{x-1}}$

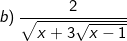
$\small b)\: \frac{2}{\sqrt{x+3\sqrt{x-1}}}$

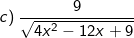
$\small c)\: \frac{9}{\sqrt{4x^2-12x+9}}$

Bài tập 7: Với giá trị nào của x thì biểu thức sau có nghĩa:

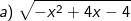
$\small a)\: \sqrt{-x^2+4x-4}$

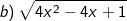
$\small b)\: \sqrt{4x^2-4x+1}$

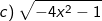
$\small c)\: \sqrt{-4x^2-1}$

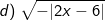
$\small d)\: \sqrt{-|2x-6|}$

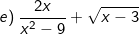
$\small e)\: \frac{2x}{x^2-9}+\sqrt{x-3}$

Việc tìm điều kiện xác định của biểu thức chứa căn là một kỹ năng nền tảng. Nắm vững cách giải các dạng bài tập cơ bản này sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán phức tạp hơn trong tương lai.