Cách giải phương trình lượng giác bậc 2 và Bài tập vận dụng - Toán 11 chuyên đề

Cách giải bài tập phương trình lượng giác bậc 2 sẽ trở thành bài toán quen thuộc khi chúng ta đặt ẩn phụ (kèm điều kiện của ẩn nếu có) rồi sau đó giải phương trình bậc 2 theo ẩn phụ này theo cách phổ biến là tính biệt số delta.

• Phương pháp giải Phương trình lượng giác bậc 2 có một hàm số lượng giác

♦ Đặt ẩn phụ t, rồi giải phương trình bậc hai đối với t, ví dụ:

 + Giải phương trình: asin²x + bsinx + c = 0;

 + Đặt t = sinx (-1≤ t ≤ 1), ta có phương trình bậc 2 ẩn t là:

 at² + bt + c = 0.

* Lưu ý: Khi đặt t = sinx (hoặc t = cosx) thì phải có điều kiện: -1 ≤ t ≤ 1.

• Bài tập Giải Phương trình lượng giác bậc 2 có một hàm số lượng giác

* Bài tập 1: Giải các phương trình lượng giác bậc 2 sau

a)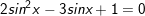 

b)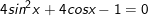 

* Lời giải:

a)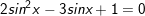 

- Đặt 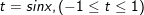 ta có:

 2t² - 3t + 1 = 0

(vì a + b + c = 0 nên ta nhẩm được nghiệm)

 ⇔ t = 1 hoặc t = 1/2.

+ Với t = 1: sinx = 1 

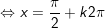
+ Với t=1/2: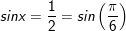  

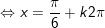  hoặc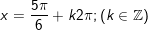 

b)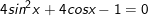 

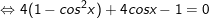
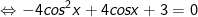
+ Đặt 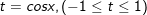 ta có:

 -4t² + 4t + 3 = 0

(tính theo biệt số delta hoặc delta', ta tìm được nghiệm)

 ⇔ t = 3/2 hoặc t = -1/2.

+ Với t = 3/2 >1 (loại)

+ Với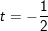    

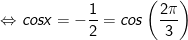
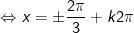
* Chú ý: Đối với phương trình dạng: asin²x + bsinx.cosx + c.cos²x = 0, (a,b,c≠0).

Phương pháp giải như sau:

 - Ta có: cosx = 0 không phải là nghiệm của phương trình vì a ≠ 0,

 Chia 2 vế cho cos²x, ta có:atan²x + btanx + c = 0 (được PT bậc 2 với tanx)

 - Nếu phương trình dạng: asin²x + bsinx.cosx + c.cos²x = d thì ta thay d = d.sin²x + d.cos²x, và rút gọn đưa về dạng trên.

* Bài tập 2: Giải các phương trình lượng giác sau:

a) 2sin²x - 3sinxcosx + cos²x = 0

b) cos²2x - 7sin4x + 3sin²2x = -3

* Lời giải:

a) 2sin²x - 3sinxcosx + cos²x = 0

Ta thấy 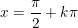 (tức cosx = 0) không phải là nghiệm của phương trình.

⇒ cosx ≠ 0, chia hai vế cho cos²x, ta được:

 2tan²x - 3tanx + 1 = 0

Đặt t = tanx, phương trình trở thành:

 2t² - 3t + 1 = 0 (có a + b + c = 0)

⇔ t = 1 hoặc t = 1/2

+ Với t = 1 ⇔ tanx = 1

 ⇔ tanx = tan(π/4) ⇔ x = π/4 + kπ (với k ∈ Z)

+ Với t = 1/2 ⇔ tanx = 1/2

 ⇔ x = arctan(1/2) + kπ (với k ∈ Z)

b) cos²2x - 7sin4x + 3sin²2x = -3

 ⇔ cos²2x - 14sin2xcos2x + 3sin²2x = -3(sin²2x + cos²2x)

 ⇔ cos²2x - 14sin2xcos2x + 3sin²2x = -3sin²2x - 3cos²2x

 ⇔ 4cos²2x - 14sin2xcos2x + 6sin²2x = 0

 ⇔ 2cos²2x - 7sin2xcos2x + 3sin²2x = 0

Ta thấy: 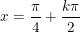 (tức cos2x = 0) không phải là nghiệm của phương trình

⇒ cos2x ≠ 0, chia hai vế cho cos2x, ta được:

 2t² - 7t + 3 = 0

(Giải phương trình bằng cách tính biệt số delta, ta được)

 ⇔ t = 3 hoặc t = 1/2

+ Với t = 3, suy ra: tan2x = 3

 ⇔ 2x = arctan3 + kπ

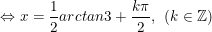
+ Với t = 1/2, suy ra: tan2x = 1/2

 ⇔ 2x = arctan(1/2) + kπ

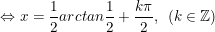
* Bài tập 3: Giải các phương trình lượng giác sau:

a) 2cos²x - 3cosx + 1 = 0

b) cot²x - 4cotx + 3 = 0

c) sin²2x - 2cos²x + 3/4 = 0

d) cos²2x + sin2x + 1 = 0

e) tan⁴x - 4tan²x + 3 = 0

* Bài tập 4: Giải các phương trình lượng giác sau:

a) sin²x - 10sinxcosx + 21cos²x = 0

b) cos²x - 3sinxcosx + 1 = 0

c) sin²2x + sin4x - 2cos²2x = 1/2

* Bài tập 5: Giải các phương trình lượng giác sau:

a) 4sin²2x - 8cos²x + 3 = 0

b) cos2x + 9cosx + 5 = 0

c) 2cos6x + tan3x - 1 = 0