Giải bài 30 trang 116 SGK Toán 9 tập 1

Bài 30 trang 116 SGK Toán 9 tập 1:

Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:

a) 

b) CD = AC + BD.

c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.

Giải bài 30 trang 116 SGK Toán 9 tập 1:

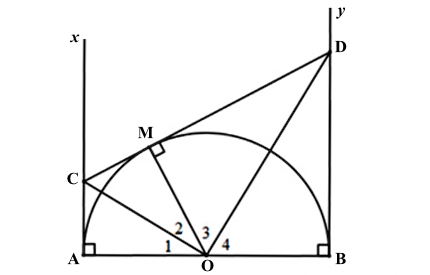
Ta có hình minh họa như sau:

[SCRIPT_ADS_IN_IMAGe]

Theo đề bài, ta có:

OA ⊥ Ax tại A, OB ⊥ By tại B

Do đó, Ax, By là các tiếp tuyến của nửa đường tròn lần lượt tại A và B

Vì CA, CM là hai tiếp tuyến của (O) lần lượt tại A và M, theo tính chất hai tiếp tuyến cắt nhau, ta có: CM = CA và 

Vì DB, DM là hai tiếp tuyến của đường tròn (O) lần lượt tại B và M, theo tính chất hai tiếp tuyến cắt nhau, ta có: DM = DB và

a) chứng minh 

Ta có: 

 (vì  và )

b) chứng minh: CD = AC + BD.

Ta có: CM = AC, MD = BD (chứng minh trên)

Lại có: CD = CM + MD = AC + BD 

Vậy CD = AC + BD (đpcm).

c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.

Ta có: CM = AC, MD = BD (chứng minh trên)

Xét tam giác COD vuông tại O có OM là đường cao (tính chất tiếp tuyến).

Áp dụng hệ thức lượng trong tam giác vuông có:

R² = MO² = MC . MD = AC . BD (do MO = R)

Vì bán kính đường tròn không đổi khi M di chuyển trên nửa đường tròn nên MO² không đổi do đó tích AC. BD không đổi khi M di chuyển trên nửa đường tròn.