Bài 8 trang 51 Toán 8 Tập 2 Chân trời sáng tạo
Hướng dẫn giải bài 8 trang 51 Toán 8 Tập 2 Chân trời Sáng tạo nội dung SGK chi tiết dễ hiểu
Bài 8 trang 51 Toán 8 Tập 2 Chân trời sáng tạo:
Cho hình thang ABCD (AB // CD). Đường thẳng song song với AB cắt AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q
Chứng minh rằng MN = PQ.
Giải bài 8 trang 51 Toán 8 Tập 2 Chân trời sáng tạo:
Ta có hình minh hoạ như sau: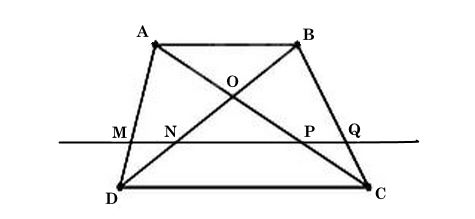
Trong ΔADB, ta có: MN // AB (gt)
Suy ra:(Hệ quả định lí Thales ) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: (Hệ quả định lí Thales ) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: (Định lí Thales ) (3)
Từ (1), (2) và (3) suy ra: .
Hay MN = PQ (đpcm)
Với nội dung bài 8 trang 51 Toán 8 tập 2 Chân trời Sáng tạo cùng cách giải bài 8 trang 51 Toán 8 Tập 2 Chân trời sáng tạo chi tiết, dễ hiểu. Hay Học Hỏi hy vọng giúp các em nắm vững phương pháp giải Toán 8 tập 2 Chân trời sáng tạo. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt.
• Xem giải bài tập SGK Toán 8 Tập 2 Chân trời sáng tạo
> Bài 2 trang 49 Toán 8 Tập 2 Chân trời sáng tạo: Tìm x trong Hình 20...
> Bài 4 trang 50 Toán 8 Tập 2 Chân trời sáng tạo: Quan sát Hình 22, chứng minh rằng MN // BC...
> Bài 5 trang 50 Toán 8 Tập 2 Chân trời sáng tạo: Tính các độ dài x, y trong Hình 23...
> Bài 9 trang 51 Toán 8 Tập 2 Chân trời sáng tạo: Quan sát Hình 25 và chứng minh...
Đánh giá & nhận xét
-
 Giải Toán 8 trang 95 tập 2 Chân trời sáng tạo
Giải Toán 8 trang 95 tập 2 Chân trời sáng tạo
-
 Bài 8 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 8 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 7 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 7 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 3 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 2 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 2 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 1 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 1 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 36 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 36 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 36 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 36 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 36 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 36 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 36 Toán 8 Tập 2 Chân trời sáng tạo: Phương Trình Bậc Nhất
Bài 3 trang 36 Toán 8 Tập 2 Chân trời sáng tạo: Phương Trình Bậc Nhất
-
 Bài 2 trang 36 Toán 8 Tập 2 Chân trời sáng tạo
Bài 2 trang 36 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 1 trang 35 Toán 8 Tập 2 Chân trời sáng tạo: Phương Trình Biểu Diễn Cân Bằng
Bài 1 trang 35 Toán 8 Tập 2 Chân trời sáng tạo: Phương Trình Biểu Diễn Cân Bằng
-
 Bài 19 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
Bài 19 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 18 trang 29 Toán 8 Tập 2 Chân trời sáng tạo: Đồ Thị Hàm Số Cắt Nhau
Bài 18 trang 29 Toán 8 Tập 2 Chân trời sáng tạo: Đồ Thị Hàm Số Cắt Nhau
-
 Bài 17 trang 29 Toán 8 Tập 2 Chân trời sáng tạo: Đồ Thị Hàm Số Bậc Nhất
Bài 17 trang 29 Toán 8 Tập 2 Chân trời sáng tạo: Đồ Thị Hàm Số Bậc Nhất
-
 Bài 16 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
Bài 16 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 15 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
Bài 15 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 14 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
Bài 14 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 13 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
Bài 13 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 12 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
Bài 12 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 11 trang 29 Toán 8 Tập 2 Chân trời sáng tạo: Hàm Số & Giá Trị Hàm Số
Bài 11 trang 29 Toán 8 Tập 2 Chân trời sáng tạo: Hàm Số & Giá Trị Hàm Số
-
 Bài 10 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
Bài 10 trang 29 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 9 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 9 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 8 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 8 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 7 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 7 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 3 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 2 trang 28 Toán 8 Tập 2 Chân trời sáng tạo: Độ dài đoạn thẳng
Bài 2 trang 28 Toán 8 Tập 2 Chân trời sáng tạo: Độ dài đoạn thẳng
-
 Bài 1 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
Bài 1 trang 28 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 10 trang 27 Toán 8 Tập 2 Chân trời sáng tạo
Bài 10 trang 27 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 9 trang 27 Toán 8 Tập 2 Chân trời sáng tạo
Bài 9 trang 27 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 8 trang 27 Toán 8 Tập 2 Chân trời sáng tạo
Bài 8 trang 27 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 7 trang 26 Toán 8 Tập 2 Chân trời sáng tạo
Bài 7 trang 26 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 26 Toán 8 Tập 2 Chân trời sáng tạo: Viết phương trình đường thẳng song song
Bài 6 trang 26 Toán 8 Tập 2 Chân trời sáng tạo: Viết phương trình đường thẳng song song


















































