Bài 15 trang 60 Toán 8 Tập 2 Chân trời sáng tạo

Bài 15 trang 60 Toán 8 Tập 2 Chân trời sáng tạo: 

Cho tứ giác ABCD có AC và BD cắt nhau tại O. Qua O, kẻ đường thẳng song song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F.

a) Chứng minh FE // BD;

b) Từ O kẻ đường thẳng song song với AB cắt BC tại G và đường thẳng song song với AD cắt CD tại H. Chứng minh rằng CG.DH = BG.CH.

Giải bài 15 trang 60 Toán 8 Tập 2 Chân trời sáng tạo: 

Ta có hình minh hoạ như sau:

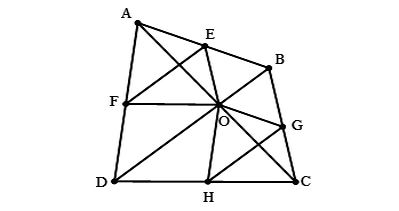
a) Tam giác ABC có OE // BC (gt)

Theo định lí Thalès, ta có:   (1)

Tam giác ADC có OF // CD (gt)

Theo định lí Thalès, ta có:  (2)

Từ (1) và (2) suy ra:

Xét Tam giác ADB có:

⇒ EF // BD (theo định lí Thalès đảo)

b) Tam giác ABC có OG // AB (gt)

Theo định lí Thalès, ta có:  (3)

Tam giác ACD có OH // AD (gt)

Theo định lí Thalès, ta có: (4)

Từ (3) (4) suy ra:

  ⇒ CG.DH = BG.CH