Giải bài 13 trang 106 SGK Toán 9 tập 1: Đường tròn và dây cung

Đề bài:

Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:

a) EH = EK

b) EA = EC.

Phân tích và Hướng dẫn giải

Để chứng minh các yêu cầu của bài toán, ta sẽ sử dụng các kiến thức sau:

1. Quan hệ đường kính và dây: Đường kính đi qua trung điểm của một dây (không đi qua tâm) thì vuông góc với dây đó.

2. Quan hệ giữa dây và khoảng cách đến tâm: Hai dây bằng nhau thì cách đều tâm.

3. Tam giác bằng nhau: Sử dụng các trường hợp bằng nhau của tam giác vuông để chứng minh hai đoạn thẳng bằng nhau.

Lời giải chi tiết bài 13 trang 106:

Ta có hình minh hoạ như sau:

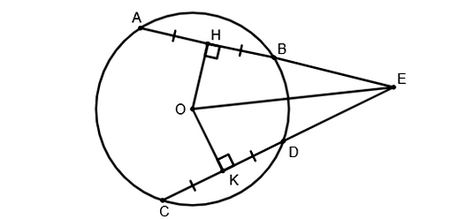
a) Chứng minh EH = EK

Nối O với E

Có HA = HB (H là trung điểm AB) => OH ⊥ AB (do đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)

Có KC = KD (K là trung điểm CD) => OK ⊥ CD (do đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)

Mặt khác, AB = CD nên OH = OK (do hai dây bằng nhau thì cách đều tâm)

Xét tam giác HOE và tam giác KOE có

OH = OK

EO chung

 (do OH ⊥ AB và OK ⊥ CD)

⇒ ΔHOE = ΔKOE theo trường hợp cạnh huyền – cạnh góc vuông.

⇒ EH = EK (*)

b) Chứng minh EA = EC.

Theo đề bài, AB = CD

Từ (*) và (**) ta có:

EH + HA = EK + KC

⇒ EA = EC (đpcm)