Cách giải phương trình trùng phương, phương trình tích - Toán lớp 9

1. Cách giải phương trình đưa về phương trình tích.

Phương pháp giải

• Bước 1: Biến đổi phương trình ban đầu bằng các phép biến đổi đại số (đặt nhân tử chung, sử dụng hằng đẳng thức, nhóm các hạng tử,...).

• Bước 2: Đưa phương trình về dạng phương trình tích $A(x)\cdot B(x)=0$.

• Bước 3: Giải phương trình bằng cách cho từng nhân tử bằng 0, tức là $A(x)=0$ hoặc $B(x)=0$.

Ví dụ 1: Giải phương trình

a) (x - 3)(x² - 3x + 2) = 0

b) x³ + 3x² - 2x - 6 = 0

Lời giải:

a) (x - 3)(x² - 3x + 2) = 0

⇔ x - 3 = 0 hoặc x² - 3x + 2 = 0

+) x - 3 = 0 ⇔ x₁ = 3

+) x² - 3x + 2 = 0 ta thấy: a = 1; b = -3; c = 2 và a + b + c = 0 nên theo Vi-et ta có nghiệm x₂ = 1; x₃ = c/a = 2.

• Kết luận: Vậy phương trình đã cho có 3 nghiệm là: x₁ = 3; x₂ = 1; x₃ = 2.

b) x³ + 3x² - 2x - 6 = 0

⇔ x²(x + 3) - 2(x + 3) = 0

⇔ (x + 3)(x² - 2) = 0

⇔ x + 3 = 0 hoặc x² - 2 = 0

+) x + 3 = 0 ⇔ x₁ = -3

+) x² - 2 = 0 ⇔  ;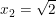 

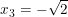
• Kết luận: Vậy phương trình đã cho có 3 nghiệm là: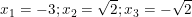

• Xem thêm: Cách giải phương trình chứa ẩn ở mẫu cực hay

* Ví dụ 2: Giải các phương trình

a) (3x² – 5x + 1)(x² – 4) = 0;

b) (2x² + x – 4)² – (2x – 1)² = 0.

° Lời giải:

a) (3x² – 5x + 1)(x² – 4) = 0;

⇔ 3x² – 5x + 1 = 0 hoặc x² – 4 = 0

+)Giải: 3x² – 5x + 1 = 0

- Có a = 3; b = -5; c = 1 ⇒ Δ = (-5)² – 4.3 = 13 > 0

⇒ Phương trình có hai nghiệm: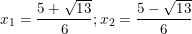 

+)Giải: x² – 4 = 0

⇔ (x - 2)(x + 2) = 0

⇔ x = 2 hoặc x = -2.

• Kết luận: Vậy phương trình đã cho có 4 nghiệm là:

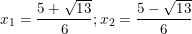 ; x₃ = 2; x₄ = -2

- Hay tập nghiệm của phương trình là: 

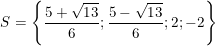
b) (2x² + x – 4)² – (2x – 1)² = 0

⇔ (2x² + x – 4 – 2x + 1)(2x² + x – 4 + 2x – 1) = 0

⇔ (2x² – x – 3)(2x² + 3x – 5) = 0

⇔ 2x² – x – 3 = 0 hoặc 2x² + 3x – 5 = 0

+) Giải: 2x² – x – 3 = 0

- Có a = 2; b = -1; c = -3 và thấy a – b + c = 0

⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 3/2.

+) Giải: 2x² + 3x – 5 = 0

- Có a = 2; b = 3; c = -5 và thấy a + b + c = 0

⇒ Phương trình có hai nghiệm x = 1 và x = c/a = -5/2.

• Kết luận: Vậy phương trình đã cho có 4 nghiệm là: x₁ = -1; x₂ =  3/2; x₃ = 1; x₄ = -5/2.

- Hay tập nghiệm của phương trình là: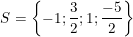 

• Xem thêm: Cách giải phương trình bâc 2 chứa ẩn ở mẫu cực hay 

2. Cách giải phương trình trùng phương ax⁴ +bx² + c = 0 (a≠0).

Phương pháp giải 1: Đặt ẩn phụ

• Bước 1: Đặt ẩn phụ t=x2 với điều kiện $t\ge 0$.

• Bước 2: Thay $t$ vào phương trình, ta được phương trình bậc hai theo $t$: at2+bt+c=0.

• Bước 3: Giải phương trình bậc hai theo $t$, sau đó đối chiếu với điều kiện $t\ge 0$.

  • Với mỗi nghiệm $t$ thỏa mãn, ta giải phương trình x2=t để tìm nghiệm $x$.

• Bước 4: Kết luận số nghiệm của phương trình trùng phương.

Phương pháp giải 2: Giải trực tiếp bằng cách đưa về phương trình tích

• Biến đổi phương trình trùng phương bằng cách phân tích thành nhân tử để đưa về dạng $A(x)\cdot B(x)=0$.

* Ví dụ 1: Giải các phương trình trùng phương:

a) x⁴ – 5x² + 4 = 0

b) 2x⁴ – 3x² – 2 = 0

c) 3x⁴ + 10x² + 3 = 0

° Lời giải:

a) x⁴ – 5x² + 4 = 0  (1)

- Đặt t = x², điều kiện t ≥ 0.

- Khi đó (1) trở thành : t² – 5t + 4 = 0 (2)

- Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm t₁ = 1; t₂ = c/a = 4

- Cả hai giá trị đều thỏa mãn điều kiện.

+ Với t = 1 ⇒ x² = 1 ⇒ x = 1 hoặc x = -1;

+ Với t = 4 ⇒ x² = 4 ⇒ x = 2 hoặc x = -2.

- Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.

b) 2x⁴ – 3x² – 2 = 0; (1)

- Đặt t = x², điều kiện t ≥ 0.

- Khi đó (1) trở thành : 2t² – 3t – 2 = 0 (2)

- Giải (2) : Có a = 2 ; b = -3 ; c = -2 ⇒ Δ = (-3)² - 4.2.(-2) = 25 > 0

⇒ Phương trình có hai nghiệm: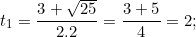  

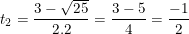
- Đối chiếu điều kiện t≥0 ta thấy chỉ có giá trị t₁ = 2 thỏa mãn điều kiện.

+ Với t = 2 ⇒ x² = 2 ⇒ x = √2 hoặc x = -√2;

- Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.

c) 3x⁴ + 10x² + 3 = 0 (1)

- Đặt t = x² , điều kiện t ≥ 0.

- Khi đó (1) trở thành : 3t² + 10t + 3 = 0 (2)

- Giải (2): Có a = 3; b' = 5; c = 3 ⇒ Δ’ = 5² – 3.3 = 16 > 0

⇒ Phương trình có hai nghiệm phân biệt:

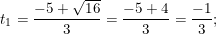
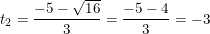
- Đối chiếu điều kiện t≥0 ta thấy cả 2 giá trị t₁ = -1/3 <0 và t₂ = -3<0 đều không thỏa điều kiện. Vậy phương trình (1) vô nghiệm.

* Ví dụ 2: Giải các phương trình trùng phương

a) 9x⁴ – 10x² + 1 = 0 

b) 5x⁴ + 2x² – 16 = 10 – x²

c) 0,3x⁴ + 1,8x² + 1,5 = 0

d)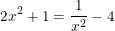 

° Lời giải:

a) 9x⁴ – 10x² + 1 = 0 (1)

- Đặt t = x², điều kiện t ≥ 0.

- Khi đó (1) trở thành : 9t² – 10t + 1 = 0 (2)

+) Giải (2): Có a = 9 ; b = -10 ; c = 1; ta thấy a + b + c = 0

⇒ Phương trình (2) có nghiệm t₁ = 1; t₂ = c/a = 1/9.

- Cả hai nghiệm đều thỏa mãn điều kiện t≥0.

+ Với t = 1 ⇒ x² = 1 ⇒ x = 1 hoặc x = -1.

+ Với t = 1/9 ⇒ x² = 1/9 ⇒ x = 1/3 hoặc x = -1/3. 

• Kết luận: Vậy phương trình (1) có tập nghiệm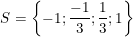 

b) 5x⁴ + 2x² – 16 = 10 – x²

⇔ 5x⁴ + 2x² – 16 – 10 + x² = 0

⇔ 5x⁴ + 3x² – 26 = 0 (1)

- Đặt t = x² , điều kiện t ≥ 0.

- Khi đó (1) trở thành : 5t² + 3t – 26 = 0 (2)

+ Giải (2): Có a = 5 ; b = 3 ; c = -26 ⇒ Δ = 3² – 4.5.(-26) = 529 > 0

⇒ Phương trình có hai nghiệm phân biệt:

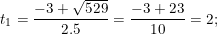
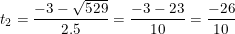
- Đối chiếu điều kiện chỉ có t₁ thỏa điều kiện, nên:

+ Với t = 2 ⇒ x² = 2 ⇒ x = √2 hoặc x = -√2.

⇒ Kết luận: Vậy phương trình (1) có tập nghiệm S = {-√2; √2}.

c) 0,3x⁴ + 1,8x² + 1,5 = 0 (1)

- Đặt t = x², điều kiện t ≥ 0.

- Khi đó, (1) trở thành : 0,3t² + 1,8t + 1,5 = 0 (2)

+ Giải (2) : có a = 0,3 ; b = 1,8 ; c = 1,5; ta thấy a – b + c = 0

⇒ Phương trình có hai nghiệm t₁ = -1 và t₂ = -c/a = -5.

- Đối chiếu với điều kiện t ≥ 0 thấy cả hai nghiệm đều không thỏa.

⇒ Vậy phương trình (1) vô nghiệm.

d)  (*)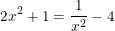

- Điều kiện xác định: x ≠ 0.

- Quy đồng, khử mẫu ta được:

(*) ⇔ 2x⁴ + x² = 1 – 4x²

 ⇔ 2x⁴ + x² + 4x² – 1 = 0

 ⇔ 2x⁴ + 5x² – 1 = 0 (1)

- Đặt t = x², điều kiện t > 0 (do x ≠ 0).

- Khi đó (1) trở thành : 2t² + 5t – 1 = 0 (2)

+ Giải (2): Có a = 2 ; b = 5 ; c = -1 ⇒ Δ = 5² – 4.2.(-1) = 33 > 0

⇒ Phương trình có hai nghiệm phân biệt:

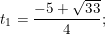
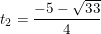
- Đối chiếu với điều kiện t >0 thấy có nghiệm t₁ thỏa mãn, nên:

+ Với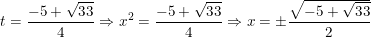 

• Kết luận: Vậy phương trình có tập nghiệm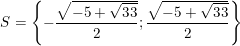

3. Bài tập vận dụng

* Bài 1: Giải các phương trình sau

a) x⁴ - 22x² - 8x +77 = 0

b) x⁴ - 6x³ + 8x² + 2x - 1 = 0

c) x⁴ + 2x³ - 5x² + 6x - 3 = 0

* Bài 2: Giải các phương trình sau

a) 5x⁴ + 3x² - 2 = 0

b) x⁴ - 5x² + 6 = 0

c) 2x⁴ - 3x² - 2 = 0