Cách giải phương trình bậc 2 chứa ẩn ở mẫu - Toán lớp 9

16:50:5928/05/2020

Chào các em! Phương trình chứa ẩn ở mẫu là một trong những dạng toán thường gặp trong chương trình Toán 9. Khi giải, các em cần hết sức cẩn thận để không mắc sai sót. Bài viết này sẽ hướng dẫn chi tiết cách giải phương trình bậc 2 chứa ẩn ở mẫu qua từng bước cụ thể và các ví dụ minh họa để các em nắm vững phương pháp.

1. Các bước giải phương trình chứa ẩn ở mẫu

Để giải một phương trình chứa ẩn ở mẫu, các em hãy thực hiện theo các bước sau:

Bước 1: Tìm điều kiện xác định (ĐKXĐ) của phương trình bằng cách cho tất cả các mẫu thức khác 0.
Bước 2: Quy đồng mẫu thức hai vế của phương trình rồi khử mẫu thức.
Bước 3: Giải phương trình vừa nhận được (thường là phương trình bậc hai hoặc bậc nhất).
Bước 4: Kiểm tra xem các nghiệm vừa tìm được có thỏa mãn ĐKXĐ không. Sau đó kết luận tập nghiệm.

2. Ví dụ minh họa

Ví dụ 1: Giải các phương trình:

a)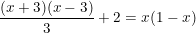 $small frac{(x+3)(x-3)}{3}+2=x(1-x)$

b)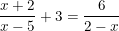 $small frac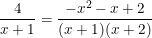{x+2}{x-5}+3=frac{6}{2-x}$

c) $small frac{4}{x+1}=frac{-x^{2}-x+2}{(x+1)(x+2)}$

Lời giải:

a)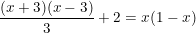 $small frac{(x+3)(x-3)}{3}+2=x(1-x)$

- Điều kiện xác định: 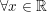small forall xin mathbb{R}

- Ta có:

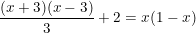
$small frac{(x+3)(x-3)}{3}+2=x(1-x)$

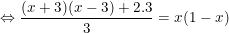
$small Leftrightarrow frac{(x+3)(x-3)+2.3}{3}=x(1-x)$

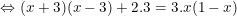
small Leftrightarrow (x+3)(x-3)+2.3=3.x(1-x)

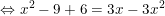
small Leftrightarrow x^2-9+6=3x-3x^2

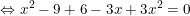
small Leftrightarrow x^2-9+6-3x+3x^2=0

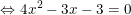
small Leftrightarrow 4x^2-3x-3=0

- Có a = 4; b = -3; c = -3 nên:

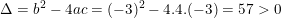
$small Delta =b^{2}-4ac=(-3)^2-4.4.(-3)=57>0$

⇒ Phương trình có 2 nghiệm phân biệt:

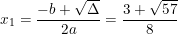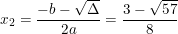
$small x_{1}=frac{-b+sqrt{Delta }}{2a}=frac{3+sqrt{57}}{8}$ ; $small x_{2}=frac{-b-sqrt{Delta }}{2a}=frac{3-sqrt{57}}{8}$

- Kết luận: Phương trình có 2 nghiệm.

b)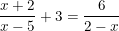 $small frac{x+2}{x-5}+3=frac{6}{2-x}$

- Điều kiện xác định: x≠5; x≠2.

- Quy đồng khử mẫu ta được:

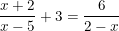
$small frac{x+2}{x-5}+3=frac{6}{2-x}$

⇔ (x+2)(2-x) + 3(2-x)(x-5) = 6(x-5)

⇔ 4 - x² + 6x - 3x² - 30 + 15x = 6x - 30

⇔ 4 - x² + 6x - 3x² - 30 + 15x - 6x + 30 = 0

⇔ -4x² + 15x + 4 = 0

- Có a = -4; b = 15; c = 4 ⇒ Δ = b² - 4ac = 15² – 4.(-4).4 = 289 > 0

⇒ Phương trình có 2 nghiệm phân biệt:

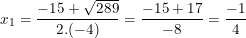$small x_{1}=frac{-15+sqrt{289}}{2.(-4)}=frac{-15+17}{-8}=frac{-1}{4}$ (thỏa)

$small x_{2}=frac{-15-sqrt{289}}{2.(-4)}=frac{-15-17}{-8}=4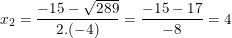$ (thỏa)

- Vậy cả hai nghiệm đều thỏa điều kiện, tập nghiệm: S={-1/4; 4}

c)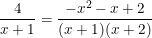 $small frac{4}{x+1}=frac{-x^{2}-x+2}{(x+1)(x+2)}$

- Điều kiện xác định: x ≠ -1; x ≠ -2.

- Quy đồng và khử mẫu ta được:

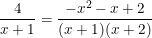
$small frac{4}{x+1}=frac{-x^{2}-x+2}{(x+1)(x+2)}$

⇔ 4.(x + 2) = -x² – x + 2

⇔ 4x + 8 = -x² – x + 2

⇔ 4x + 8 + x² + x – 2 = 0

⇔ x² + 5x + 6 = 0.

- Có a = 1; b = 5; c = 6 ⇒ Δ = 5² – 4.1.6 = 1 > 0

⇒ Phương trình có hai nghiệm phân biệt:

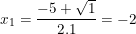$small x_{1}=frac{-5+sqrt{1}}{2.1}=-2$ (loại); 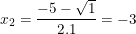$small x_{2}=frac{-5-sqrt{1}}{2.1}=-3$ (thỏa)

- Chỉ có nghiệm x₂ = -3 thỏa mãn, nên kết luận phương trình có nghiệm x=-3.

• Xem thêm: Cách giải phương trình chứa dấu giá trị tuyệt đối và có tham số cực hay

3. Bài tập phương trình bậc 2 chứa ẩn ở mẫu

Bài tập 1: Giải phương trình sau: 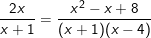$small frac{2x}{x+1}=frac{x^2-x+8}{(x+1)(x-4)}$

Bài tập 2: Giải phương trình sau: 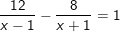$small frac{12}{x-1}-frac{8}{x+1}=1$

Bài tập 3: Giải phương trình sau: 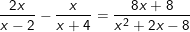$small frac{2x}{x-2}-frac{x}{x+4}=frac{8x+8}{x^2+2x-8}$

Hy vọng với bài viết về cách giải phương trình bậc 2 chứa ẩn ở mẫu, các em đã hiểu rõ hơn về các bước giải bài toán dạng này. Hãy luôn nhớ thực hiện các bước một cách cẩn thận, đặc biệt là bước tìm điều kiện xác định.