Tích phân từng phần, Công thức cách tính và Bài tập có lời giải - Toán lớp 12

14:43:1921/12/2020

Nguyên hàm tích phân là một trong những nội dung quan trọng thường xuất hiện trong đề thi tốt nghiệp THPT quốc gia để xét vào đại học. Nếu đã nắm vững phần nguyên hàm thì việc tính tích phân xác định với phương pháp tích phân từng phần sẽ rất dễ dàng với các em.

Vậy công thức cách tính Tích phân từng phần như thế nào? Bài viết dưới đây, chúng ta sẽ cùng tìm hiểu các dạng bài tập tính tích phân xác định mà ta phải vận dụng phương pháp tích phân từng phần để giải, qua đó, giải các bài tập minh họa để các em hiểu rõ hơn.

» Đừng bỏ lỡ: Tính tích phân bằng phương pháp Đổi biến số và Bài tập có lời giải chi tiết, dễ hiểu

I. Tích phân từng phần, công thức, cách tính

• Nếu u(x) và v(x) là các hàm số có đạo hàm và liên tục trên [a;b] thì:

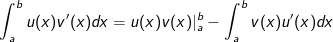
$\int_{a}^{b}u(x)v'(x)dx=u(x)v(x)|_{a}^{b}-\int_{a}^{b}v(x)u'(x)dx$

hay 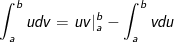$\int_{a}^{b}udv=uv|_{a}^{b}-\int_{a}^{b}vdu$

• Áp dụng công thức trên ta có cách tính tích phân từng phần như sau:

- Bước 1: Viết f(x)dx dưới dạng udv = uv'dx bằng cách chọn một phần thích hợp của f(x) làm u(x) và phần còn lại dv = v'(x)dx.

- Bước 2: Tính du = u'dx và v = ∫dv = ∫v'(x)dx

- Bước 3: Tính 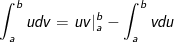$\int_{a}^{b}udv=uv|_{a}^{b}-\int_{a}^{b}vdu$

> Lưu ý: Phương pháp tích phân từng phần thường được vận dụng khi hàm dưới dấu tích phân là tích của hai loại hàm số khác nhau (đa thức - logarit, đa thức - lượng giác, lượng giác - hàm mũ,...).

II. Một số dạng bài tập vận dụng tích phân từng phần thường gặp

• Tính tích phân hàm đa thức P(x) và hàm logarit nepe (lnx): 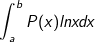$\int_{a}^{b}P(x)lnxdx$

- Ta đặt u = lnx, dv = P(x)dx

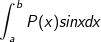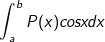
• Tính tích phân hàm đa thức P(x) và hàm lượng giác (sinx; cosx): $\int_{a}^{b}P(x)sinxdx$ hoặc $\int_{a}^{b}P(x)cosxdx$

- Ta đặt u = P(x), dv = sinxdx (hoặc dv = cosxdx)

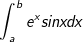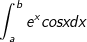
• Tính tích phân hàm mũ (e^x) và hàm lượng giác (sinx; cosx): $\int_{a}^{b}e^{x}sinxdx$ hoặc $\int_{a}^{b}e^{x}cosxdx$

- Ta đặt u = e^x , dv = sinxdx (hoặc dv = cosxdx). Tính hai lần

• Tính tích phân hàm mũ (e^x) và hàm đa thức P(x): 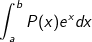$\int_{a}^{b}P(x)e^xdx$

- Ta đặt u = P(x) , dv = e^xdx

III. Bài tập tích phân từng phần có lời giải

* Bài tập 1: Tính các tích phân sau bằng phương pháp tích phân từng phần

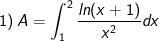
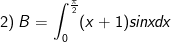
$1)\:A= \int_{1}^{2}\frac{ln(x+1)}{x^2}dx$ $2)\: B=\int_{0}^{\frac{\pi }{2}}(x+1)sinxdx$

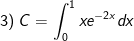
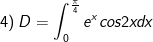
$3)\: C=\int_{0}^{1}xe^{-2x}dx$ $4)\: D=\int_{0}^{\frac{\pi }{4}}e^{x}cos2xdx$

* Lời giải:

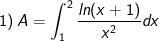
$1)\:A= \int_{1}^{2}\frac{ln(x+1)}{x^2}dx$

Đặt 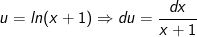$u=ln(x+1)\Rightarrow du=\frac{dx}{x+1}$

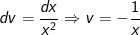
$dv=\frac{dx}{x^2}\Rightarrow v=-\frac{1}{x}$

- Áp dụng công thức tích phân từng phần, ta có:

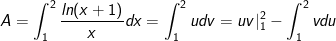
$A=\int_{1}^{2}\frac{ln(x+1)}{x}dx=\int_{1}^{2}udv=uv|_{1}^{2}-\int_{1}^{2}vdu$

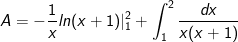
$A=-\frac{1}{x}ln(x+1)|_{1}^{2}+\int_{1}^{2}\frac{dx}{x(x+1)}$

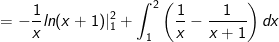
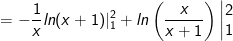
$=-\frac{1}{x}ln(x+1)|_{1}^{2}+\int_{1}^{2}\left ( \frac{1}{x}-\frac{1}{x+1} \right )dx$ $=-\frac{1}{x}ln(x+1)|_{1}^{2}+ln\left ( \frac{x}{x+1} \right )\left |\begin{matrix} 2\\ 1 \end{matrix} \right.$

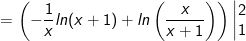
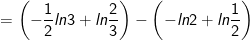
$=\left (-\frac{1}{x}ln(x+1)+ln\left ( \frac{x}{x+1} \right ) \right )\left |\begin{matrix} 2\\ 1 \end{matrix} \right.$ $=\left (-\frac{1}{2}ln3+ln\frac{2}{3} \right )-\left (-ln2+ln\frac{1}{2} \right )$

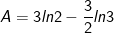
$A=3ln2-\frac{3}{2}ln3$

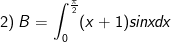
$2)\: B=\int_{0}^{\frac{\pi }{2}}(x+1)sinxdx$

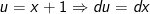
- Đặt $u=x+1\Rightarrow du=dx$

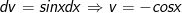
$dv=sinxdx \Rightarrow v=-cosx$

- Áp dụng công thức tích phân từng phần ta được:

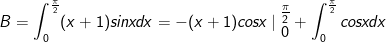
$B=\int_{0}^{\frac{\pi }{2}}(x+1)sinxdx=-(x+1)cosx\left | \right. \begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix}+\int_{0}^{\frac{\pi }{2}}cosxdx$

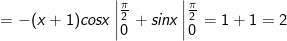
$=-(x+1)cosx\left |\begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix} \right.+sinx\left |\begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix} \right.=1+1=2$

Vậy B = 2.

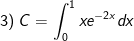
$3)\: C=\int_{0}^{1}xe^{-2x}dx$

- Đặt 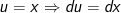$u=x\Rightarrow du=dx$

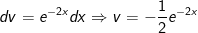
$dv=e^{-2x}dx\Rightarrow v=-\frac{1}{2}e^{-2x}$

- Áp dụng công thức tính tích phân từng phần ta được

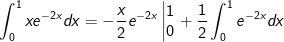
$\int_{0}^{1}xe^{-2x}dx=-\frac{x}{2}e^{-2x}\left |\begin{matrix} 1\\ 0 \end{matrix} \right.+\frac{1}{2}\int_{0}^{1}e^{-2x}dx$

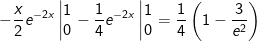
$-\frac{x}{2}e^{-2x}\left |\begin{matrix} 1\\ 0 \end{matrix} \right.-\frac{1}{4}e^{-2x}\left |\begin{matrix} 1\\ 0 \end{matrix} \right.=\frac{1}{4}\left ( 1-\frac{3}{e^2} \right )$

Vậy 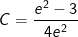$C=\frac{e^2-3}{4e^2}$

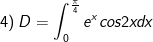
$4)\: D=\int_{0}^{\frac{\pi }{4}}e^{x}cos2xdx$

- Đặt 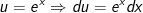$u=e^x\Rightarrow du=e^xdx$

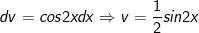
$dv=cos2xdx\Rightarrow v=\frac{1}{2}sin2x$

- Áp dụng công thức tích phân từng phần ta được:

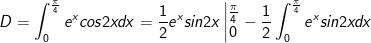
$D=\int_{0}^{\frac{\pi }{4}}e^xcos2xdx=\frac{1}{2}e^xsin2x\left|\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.-\frac{1}{2}\int_{0}^{\frac{\pi }{4}}e^xsin2xdx$

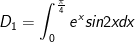
- Xét: $D_1=\int_{0}^{\frac{\pi }{4}}e^xsin2xdx$

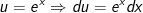
- Đặt $u=e^x\Rightarrow du=e^xdx$

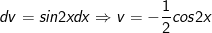
$dv=sin2xdx\Rightarrow v=-\frac{1}{2}cos2x$

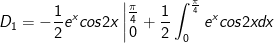
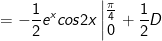
$D_1=-\frac{1}{2}e^xcos2x\left |\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.+\frac{1}{2}\int_{0}^{\frac{\pi }{4}}e^xcos2xdx$ $=-\frac{1}{2}e^xcos2x\left |\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.+\frac{1}{2}D$

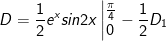
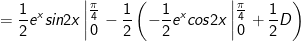
$D=\frac{1}{2}e^xsin2x\left|\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.-\frac{1}{2}D_1$ $=\frac{1}{2}e^xsin2x\left|\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.-\frac{1}{2}\left (-\frac{1}{2}e^xcos2x\left |\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.+\frac{1}{2}D \right )$

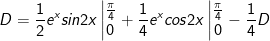
$D=\frac{1}{2}e^xsin2x\left|\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.+\frac{1}{4}e^xcos2x\left |\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.-\frac{1}{4}D$

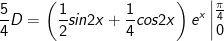
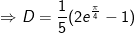
$\frac{5}{4}D=\left (\frac{1}{2}sin2x+\frac{1}{4}cos2x \right )e^x\left |\begin{matrix} \frac{\pi }{4}\\ 0 \end{matrix} \right.$ $\Rightarrow D=\frac{1}{5}(2e^{\frac{\pi }{4}}-1)$

* Bài tập 2: Tính tích phân sau:

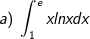
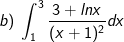
$a)\: \int_{1}^{e}xlnxdx$ $b)\: \int_{1}^{3}\frac{3+lnx}{(x+1)^2}dx$

* Lời giải:

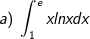
$a)\: \int_{1}^{e}xlnxdx$

- Ta đặt: 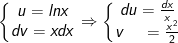$\left\{\begin{matrix} u=lnx\\ dv=xdx \end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dx}{x}\\ v\: \: \: \: \: =\frac{x^2}{2} \end{matrix}\right.$

- Khi đó, ta có:

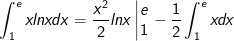
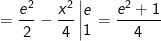
$\int_{1}^{e}xlnxdx = \frac{x^2}{2}lnx\left |\begin{matrix} e\\ 1 \end{matrix} \right.-\frac{1}{2}\int_{1}^{e}xdx$ $=\frac{e^2}{2}-\frac{x^2}{4}\left|\begin{matrix} e\\ 1 \end{matrix} \right.=\frac{e^2+1}{4}$

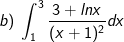
$b)\: \int_{1}^{3}\frac{3+lnx}{(x+1)^2}dx$

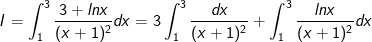
- Ta có: $I= \int_{1}^{3}\frac{3+lnx}{(x+1)^2}dx=3\int_{1}^{3}\frac{dx}{(x+1)^2}+\int_{1}^{3}\frac{lnx}{(x+1)^2}dx$

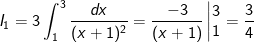
$I_1=3\int_{1}^{3}\frac{dx}{(x+1)^2}=\frac{-3}{(x+1)}\left |\begin{matrix} 3\\ 1 \end{matrix} \right.=\frac{3}{4}$

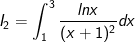
$I_2=\int_{1}^{3}\frac{lnx}{(x+1)^2}dx$

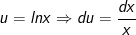
- Ta đặt: $u= lnx\Rightarrow du=\frac{dx}{x}$

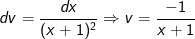
$dv=\frac{dx}{(x+1)^2}\Rightarrow v=\frac{-1}{x+1}$

- Áp dụng công thức tích phân từng phần, ta được:

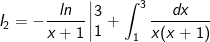
$I_2=-\frac{ln}{x+1}\left |\begin{matrix} 3\\ 1 \end{matrix} \right.+\int_{1}^{3}\frac{dx}{x(x+1)}$

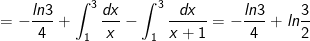
$=-\frac{ln3}{4}+\int_{1}^{3}\frac{dx}{x}-\int_{1}^{3}\frac{dx}{x+1}=-\frac{ln3}{4}+ln\frac{3}{2}$

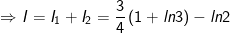
$\Rightarrow I=I_1+I_2=\frac{3}{4}\left ( 1+ln3 \right )-ln2$

* Bài tập 3: Tích các tích phân

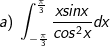
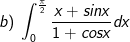
$a)\:\int_{-\frac{\pi }{3}}^{\frac{\pi }{3}}\frac{xsinx}{cos^2x}dx$ $b)\: \int_{0}^{\frac{\pi }{2}}\frac{x+sinx}{1+cosx}dx$

* Lời giải:

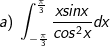
$a)\:\int_{-\frac{\pi }{3}}^{\frac{\pi }{3}}\frac{xsinx}{cos^2x}dx$

- Đặt 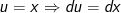$u=x\Rightarrow du=dx$

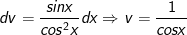
$dv=\frac{sinx}{cos^2x}dx\Rightarrow v=\frac{1}{cosx}$

- Áp dụng công thức tích phân từng phần:

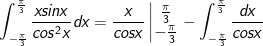
$\int_{-\frac{\pi }{3}}^{\frac{\pi }{3}}\frac{xsinx}{cos^2x}dx=\frac{x}{cosx}\left |\begin{matrix} \frac{\pi }{3}\\ -\frac{\pi }{3} \end{matrix} \right.-\int_{-\frac{\pi }{3}}^{\frac{\pi }{3}}\frac{dx}{cosx}$

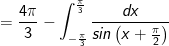
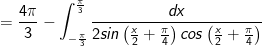
$=\frac{4\pi }{3}-\int_{-\frac{\pi }{3}}^{\frac{\pi }{3}}\frac{dx}{sin\left ( x+\frac{\pi }{2} \right )}$ $=\frac{4\pi }{3}-\int_{-\frac{\pi }{3}}^{\frac{\pi }{3}}\frac{dx}{2sin\left ( \frac{x}{2}+\frac{\pi }{4} \right ) cos\left ( \frac{x}{2}+\frac{\pi }{4} \right )}$

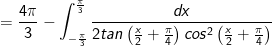
$=\frac{4\pi }{3}-\int_{-\frac{\pi }{3}}^{\frac{\pi }{3}}\frac{dx}{2tan\left ( \frac{x}{2}+\frac{\pi }{4} \right ) cos^2\left ( \frac{x}{2}+\frac{\pi }{4} \right )}$ $=\frac{4\pi }{3}-\int_{-\frac{\pi }{3}}^{\frac{\pi }{3}}\frac{d\left [tan\left ( \frac{x}{2}+\frac{\pi }{4} \right ) \right ]}{tan\left ( \frac{x}{2}+\frac{\pi }{4} \right )}$

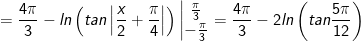
$=\frac{4\pi }{3}-ln\left ( tan\left | \frac{x}{2}+\frac{\pi }{4} \right | \right )\left |\begin{matrix} \frac{\pi }{3}\\ -\frac{\pi }{3} \end{matrix} \right.=\frac{4\pi }{3}-2ln\left ( tan\frac{5\pi }{12} \right )$

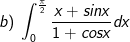
$b)\: \int_{0}^{\frac{\pi }{2}}\frac{x+sinx}{1+cosx}dx$

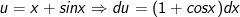
- Đặt $u=x+sinx\Rightarrow du=(1+cosx)dx$

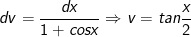
$dv=\frac{dx}{1+cosx}\Rightarrow v=tan\frac{x}{2}$

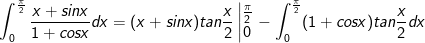
$\int_{0}^{\frac{\pi }{2}}\frac{x+sinx}{1+cosx}dx=(x+sinx)tan\frac{x }{2}\left |\begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix} \right.-\int_{0}^{\frac{\pi }{2}}(1+cosx)tan\frac{x}{2}dx$

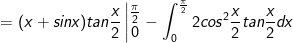
$=(x+sinx)tan\frac{x}{2}\left|\begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix} \right.-\int_{0}^{\frac{\pi }{2}}2cos^2\frac{x}{2}tan\frac{x}{2}dx$

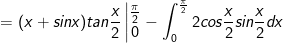
$=(x+sinx)tan\frac{x}{2}\left|\begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix} \right.-\int_{0}^{\frac{\pi }{2}}2cos\frac{x}{2}sin\frac{x}{2}dx$

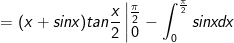
$=(x+sinx)tan\frac{x}{2}\left |\begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix} \right.-\int_{0}^{\frac{\pi }{2}}sinxdx$

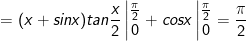
$=(x+sinx)tan\frac{x}{2}\left |\begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix} \right.+cosx\left |\begin{matrix} \frac{\pi }{2}\\ 0 \end{matrix} \right.=\frac{\pi }{2}$

IV. Bài tập tích phân từng phần tự giải

* Bài tập 1: Tính các tích phân sau:

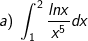
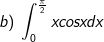
$a)\: \int_{1}^{2}\frac{lnx}{x^5}dx$ $b)\: \int_{0}^{\frac{\pi }{2}}xcosxdx$

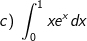
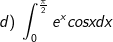
$c)\: \int_{0}^{1}xe^xdx$ $d)\: \int_{0}^{\frac{\pi }{2}}e^xcosxdx$

* Bài tập 2: Tính các tích phân sau:

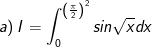
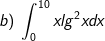
$a)\: I=\int_{0}^{\left (\frac{\pi }{2} \right )^2}sin\sqrt{x}dx$ $b)\: \int_{0}^{10}xlg^{2}xdx$

* Hướng dẫn:

a) Đặt 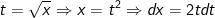$t=\sqrt{x}\Rightarrow x=t^2\Rightarrow dx=2tdt$ sau đó đổi cận và vận dụng tích phân từng phần.

b) Ta có: 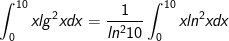$\int_{0}^{10}xlg^2xdx=\frac{1}{ln^210}\int_{0}^{10}xln^2xdx$ sau đó vận dụng tích phân từng phần.

* Bài tập 3: Tính các tính phân sau:

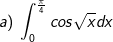
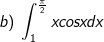
$a)\: \int_{0}^{\frac{\pi }{4}}cos\sqrt{x}dx$ $b)\: \int_{1}^{\frac{\pi }{2}}xcosxdx$

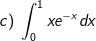
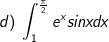
$c)\: \int_{0}^{1}xe^{-x}dx$ $d)\: \int_{1}^{\frac{\pi }{2}}e^xsinxdx$

* Bài tập 4: Tính các tính phân sau:

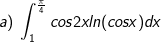
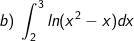
$a)\: \int_{1}^{\frac{\pi }{4}}cos2xln(cosx)dx$ $b)\: \int_{2}^{3}ln(x^2-x)dx$

* Hướng dẫn:

a) Đặt u = ln(cosx)dx → du = (-sinx/cosx)dx,

dv = cos2xdx → v = sin2x/2

b) Đặt u = ln(x² - x) → du =?; dv = dx → v = ?

Như vậy, với nội dung bài viết về tích phân từng phần và bài tập có lời giải ở trên, việc quan trọng nhất là các em cần nhớ đặt u là gì và dv là gì để thuận tiện việc tính được du và chọn nguyên hàm v. Thông thường nếu đặt đúng u và dv thì ta sẽ thấy tích phân thu được sẽ dễ tính hơn, nếu đặt sai thì tích phân thu được sẽ khó hơn tích phân ban đầu.

Tích phân từng phần, Công thức cách tính và Bài tập có lời giải - Toán lớp 12

Tags:

Đánh giá & nhận xét