Giải bài 25 trang 112 SGK Toán 9 tập 1

Bài 25 trang 112 SGK Toán 9 tập 1:

Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.

a) Tứ giác OCAB là hình gì? Vì sao?

b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.

Giải bài 25 trang 112 SGK Toán 9 tập 1:

Ta có hình minh họa như sau:

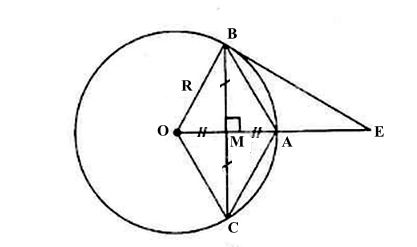
a) Tứ giác OCAB là hình gì? Vì sao?

Bán kính OA vuông góc với BC nên MB = MC.

Lại có MO = MA (gt).

Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.

Lại có: OA ⊥ BC nên OBAC là hình thoi.

b) Tính độ dài BE theo R.

Do ABOC là hình thoi nên BA = BO

Ta lại có BO = OA = R

Do đó: OB = OA = BA

• Xét ΔABO có: OB = OA = BA (chứng minh trên)

Do đó, ΔABO là tam giác đều.

Ta có EB là tiếp tuyến của (O) tại B ⇒ EB ⊥ BO

• Xét ΔBOE vuông tại B (vì )

Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ta có: