Cách tìm cực trị của hàm số bậc 2 (tìm cực đại, cực tiểu của hàm số bậc 2) - Toán 12 chuyên đề

Vậy cách tìm cực trị của hàm số bậc 2 (tìm cực đại, cực tiểu của hàm số bậc 2) như thế nào? Chúng ta hãy cùng tìm hiểu qua bài viết dưới đây. Đồng thời, qua bài viết này các em dễ dàng trả lời được các câu hỏi như: Hàm số bậc 2 có mấy cực trị? Điều kiện để hàm số bậc 2 có cực trị?...

° Cách tìm cực trị của hàm số bậc 2 (tìm cực đại, cực tiểu của hàm số bậc 2)

* Xét hàm số bậc hai: y = ax² + bx + c (a≠0)

- Bước 1: TXĐ: D = R

- Bước 2: Tính y' = 2ax + b

- Bước 3: Lập bảng biến thiên

- Từ bảng biến thiên, ta thấy y' đổi dấu khi x qua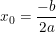 

⇒ Hàm số đạt cực trị tại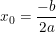 

- Nếu a<0 hàm số bậc 2 đạt cực đại

- Nếu a>0 hàm số bậc 2 đạt cực tiểu

* Ví dụ: Tìm các điểm cực trị của hàm số bậc 2: f(x) = -x² + 1

* Lời giải:

- TXĐ: D = R

- Ta có: f'(x) = -2x; f'(x) = 0 ⇔ x = 0

- Bảng biến thiên: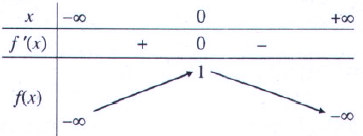- Từ bảng biến thiên suy ra x = 0 là điểm cực đại của hàm số. Đồ thị hàm số có một điểm cực đại là (0;1).

* Ví dụ 2: Tìm cực trị của hàm số bậc 2: f(x) = x² - 4x + 3

* Lời giải:

- TXĐ: D = R

- Ta có: f'(x) = 2x - 4; f'(x) = 0 ⇔ x = 2

- Bảng biến thiên: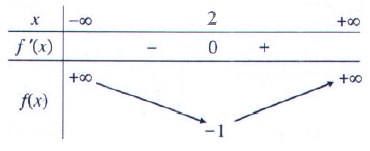- Từ bảng biến thiên suy ra x = 2 là điểm cực tiểu của hàm số. Đồ thị hàm số có một điểm cực tiểu là (2;-1).