Giải bài 2 trang 108 Toán 8 Tập 1 SGK Cánh Diều

Bài 2 trang 108 Toán 8 Tập 1 Cánh Diều:

Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành.

Giải bài 2 trang 108 Toán 8 Tập 1 Cánh Diều:

Ta có hình minh hoạ như sau:

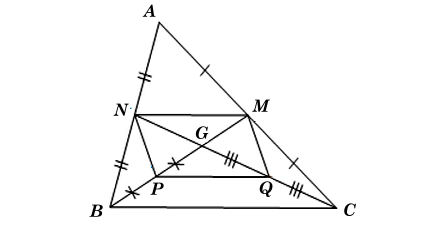
• Xét ΔABC có hai đường trung tuyến BM và CN cắt nhau tại G (giả thiết) nên G là trọng tâm của ΔABC.

Tính chất trọng tâm của tam giác, ta có:

 (*)

Mà theo bài ra:

P là trung điểm của GB nên:   (**)

Q là trung điểm của GC nên:  (***)

Từ (*), (**) và (***) suy ra:  GM = GP và GN = GQ.

• Xét tứ giác PQMN có: GM = GP và GN = GQ (chứng minh trên)

Vì tứ giác PQMN có hai đường chéo MP và NQ cắt nhau tại trung điểm G của mỗi đường nên PQMN là hình bình hành.