Tìm điều kiện m để hàm số đồng biến, nghịch biến trên khoảng (a,b) cho trước - Toán 12 chuyên đề
Xét tính đồng biến, nghịch biến của hàm số có chứa tham số đòi hỏi các em hiểu rõ và đầy đủ nội dung về hàm số, bởi dạng bài tập này mang tính bao quát cao.
Bài viết này chúng ta sẽ cùng tìm hiểu cách giải dạng bài tập: Tìm điều kiện m để hàm số đồng biến, nghịch biến trên khoảng (a; b) cho trước (xác định điều kiện tham số m để hàm số đồng biến, nghịch biến trên khoảng cho trước).
» Đừng bỏ lỡ: Các dạng bài tập về tính đơn điệu của hàm số cực hay
I. Hàm số đồng biến, nghịch biến khi nào?
1. Định nghĩa tính đơn điệu của hàm số
• Cho hàm số y = f(x) xác định trên K (với K là một khoảng hoặc một đoạn hoặc nửa khoảng).
- Hàm số y = f(x) là đồng biến (tăng) trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).
- Hàm số y = f(x) là nghịch biến (giảm) trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) > f(x2).
• Hàm đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.

2. Điều kiện cần và đủ để hàm số đơn điệu
a) Điều kiện cần để hàm số đơn điệu:
• Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
- Nếu hàm số đồng biến trên khoảng K thì f'(x) ≥ 0, ∀x ∈ K và f'(x) = 0 xảy ra tại một số hữu hạn điểm.
- Nếu hàm số nghịch biến trên khoảng K thì f'(x) ≤ 0, ∀x ∈ K và f'(x) = 0 xảy ra tại một số hữu hạn điểm.
b) Điều kiện đủ để hàm số đơn điệu
• Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
- Nếu f'(x) > 0, ∀x ∈ K thì hàm số đồng biến trên khoảng K
- Nếu f'(x) < 0, ∀x ∈ K thì hàm số nghịch biến trên khoảng K
- Nếu f'(x) = 0, ∀x ∈ K thì hàm số không đổi trên khoảng K
II. Cách tìm và xác định m để hàm số đồng biến, nghịch biến trên khoảng cho trước
* Phương pháp :
+ Bước 1: Kiểm tra tập xác định: Vì bài toán có tham số nên ta cần tìm điều kiện của tham số để hàm số xác định trên khoảng (a;b).
+ Bước 2: Tính f'(x) và tìm điều kiện của tham số để f'(x) ≥ 0 hoặc f'(x) ≤ 0 trên khoảng (a;b) theo yêu cầu bài toán.
III. Bài tập tìm (xác định) m để hàm số đồng biến, nghịch biến trên khoảng cho trước
* Bài tập 1: Cho hàm số f(x) = x3 - 3x2 - 3(m + 1)x - (m+1) (*)
a) Tìm m để hàm số đồng biến trên [1;+∞).
b) Tìm m để hàm số đồng biến trên [-1;3].
* Lời giải:
- TXĐ: D = R
- Ta có: f'(x) = 3x2 - 6x - 3(m + 1)
a) Tìm m để hàm số đồng biến trên [1;+∞).
- Để hàm số đồng biến trên [1;+∞) thì f'(x)≥0, ∀x ∈ [1;+∞).
⇒ 3x2 - 6x - 3(m + 1) ≥ 0, ∀x ∈ [1;+∞)
⇒ x2 - 2x - m - 1 ≥ 0, ∀x ∈ [1;+∞)
⇒ x2 - 2x - 1 ≥ m, ∀x ∈ [1;+∞)
- Đặt y(x) = x2 - 2x - 1 ⇒ y' = 2x - 2
- Cho y' = 0 ⇒ x = 1. Ta có bảng biến thiên sau:
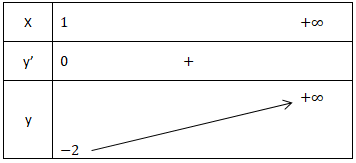
- Từ bảng biến thiên ta có: 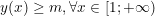
![small Rightarrow underset{xin [1;+infty )}{Min[y(x)]}=-2geq m Rightarrow mleq -2](https://hayhochoi.vn/uploads/news/wyswyg/2021_08/1625282906dfd3ug4s6m_1628420394.gif)
- Kết luận: Vậy với m ≤ -2 thì hàm số (*) đồng biến trên khoảng [1;+∞).
b) Tìm m để hàm số đồng biến trên [-1;3].
- Để hàm số nghịch biến trên [-1;3] thì f'(x)≤0, ∀x ∈ [-1;3].
⇒ 3x2 - 6x - 3(m + 1) ≤ 0,∀x ∈ [-1;3].
⇒ x2 - 2x - m - 1 ≤ 0, ∀x ∈ [-1;3].
⇒ x2 - 2x - 1 ≤ m, ∀x ∈∀x ∈ [-1;3].
- Đặt y(x) = x2 - 2x - 1 ⇒ y'(x) = 2x - 2
- Cho y'(x) = 0 ⇒ x = 1. Ta có bảng biến thiên sau:
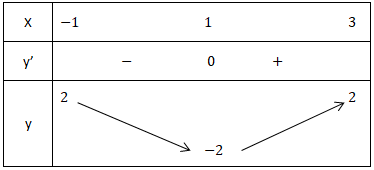
- Từ bảng biến thiên ta có: ![small y(x)leq m,forall xin [-1;3]](https://hayhochoi.vn/uploads/news/wyswyg/2021_08/1625282906qw99vo99tx_1628420399.gif)
![small Rightarrow underset{xin [-1;3]}{Max[y(x)]}=2leq mRightarrow mgeq 2](https://hayhochoi.vn/uploads/news/wyswyg/2021_08/1625282906bh43wdxd7l_1628420400.gif)
- Kết luận: Vậy với m ≥ 2 thì hàm số (*) đồng biến trên khoảng [-1;3].
* Bài tập 2: Cho hàm số: (*)
Tìm m để hàm số đồng biến trên (0;+∞)
* Lời giải:
- TXĐ: mx + 1 ≠ 0
- Ta có:
Để hàm số đồng biến trên khoảng (0;+∞) thì ta phải có y'≥0 ∀x∈(0;+∞)
Ta xét 2 trường hợp sau:
+ TH1: Với m = 0 thì hàm số (*) trở thành: y = x tăng trên (0;+∞)
+ TH2: Với m ≠ 0, y'≥0 ∀x∈(0;+∞)
Xét g(x) = m2x2 + 2mx + 1 - m2 có
Δ' = m4 > 0
Nên y'≥0 ∀x∈(0;+∞) khi và chỉ khi: x1 < x2 ≤ 0
* Lưu ý: Theo Vi-et với x1, x2 là nghiệm của phương trình bậc 2 thì:
Trong điều kiện ở trên: P≥0 để 2 nghiệm của pt bậc 2 cùng dấu; S<0 để 2 nghiệm của pt bậc 2 nằm về bên trái số 0 (cùng âm).
→ Kết luận: Kết hợp 2 trường hợp trên ta được:
Khi 0 ≤ m ≤ 1 thì hàm số (*) đồng biến trên (0;+∞)
* Bài tập 3: Cho hàm số:
Tìm m để hàm số đồng biến trên khoảng (0;3)
* Bài tập 4: Cho hàm số:
Xác định m để hàm số nghịch biến trên khoảng (0;2)
* Bài tập 5: Cho hàm số:
Xác định m để hàm số nghịch biến trên khoảng (0;+∞)
Hy vọng với bài viết về cách tìm điều kiện m để hàm số đồng biến, nghịch biến trên khoảng cho trước ở trên giúp ích cho các em. Mọi góp ý và thắc mắc các em hãy để lại phần bình luận dưới bài viết để Hay-Học-Hỏi.Vn ghi nhận và hỗ trợ, chúc các em học tập tốt.
Đánh giá & nhận xét


-
 Bài 7 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 7 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 6 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 6 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 5 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 5 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 4 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 4 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 3 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 3 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 2 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 2 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 1 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 1 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ
Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ


















































