Quy tắc 3 điểm, Quy tắc hình bình hành, Tổng và hiệu của hai Vectơ và tính chất Vectơ? Toán 10 chân trời tập 1 chương 5 bai 2

Bạn có thắc mắc: "Quy tắc 3 điểm và quy tắc hình bình hành, tính chất phép cộng vectơ, vectơ trung điểm đoạn thẳng và trọng tâm tam giác như thế nào?". Câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Tổng của hai vectơ

Cho hai vectơ  và

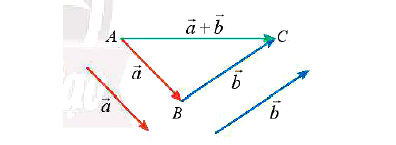
Từ một điểm A tùy ý, lấy hai điểm B, C sao cho , . Khi đó được gọi là tổng của hai vectơ  và  và được kí hiệu là 

Vậy

Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.

• Quy tắc 3 điểm của vectơ

Với ba điểm M, N, P, ta có 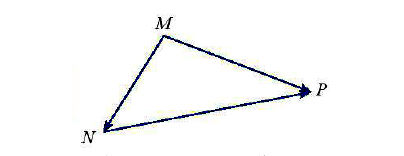* Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.

* Ví dụ: Cho hình bình hành ABCD (Hình 4). Chứng minh rằng 

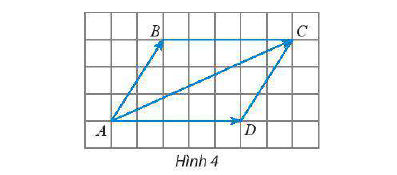
* Lời giải:

Vì ABCD là hình bình hành nên

Khi đó ta có:  (theo quy tắc ba điểm).

Vậy 

• Quy tắc hình bình hành (vectơ)

Nếu OACB là hình bình hành thì ta có:

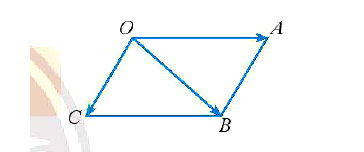
* Ví dụ: Tính tổng hai vectơ  và  trong hình 6

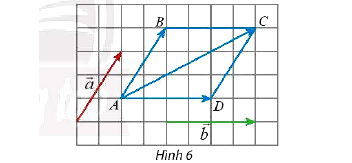
* Lời giải:

Ta có , 

Suy ra: 

Theo quy tắc hình bình hành, ta có:

Vậy 

2. Tính chất của phép cộng các vectơ

Phép cộng vectơ có các tính chất sau:

+ Tính chất giao hoán: 

+ Tính chất kết hợp: 

+ Với mọi vectơ , ta luôn có: 

* Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ  kí hiệu là  với 

* Chú ý: Cho vectơ tuỳ ý 

Ta có

3. Hiệu của hai vectơ

Cho hai vectơ  và 

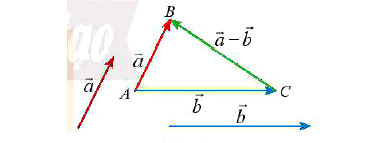
Hiệu của hai vectơ  và là vectơ  và kí hiệu là 

Phép toán tìm hiệu của hai vectơ được gọi là phép trừ vectơ.

* Chú ý: Cho ba điểm O, A, B, ta có: 

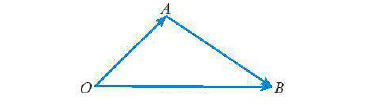
* Ví dụ: Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:

a) 

b) 

* Lời giải:

Ta có hình vẽ minh họa như sau: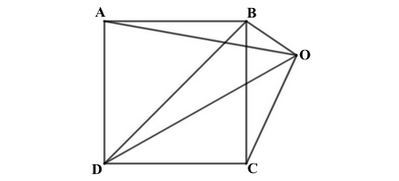a) Với ba điểm O, B , D ta có

Do đó:

Mà BD là đường chéo của hình vuông có cạnh bằng 1 nên BD = 

Vậy

b) Ta có: 

Vậy

4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi 

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi

* Ví dụ: Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

a) 

b)

c) 

* Lời giải:

Ta có hình minh họa như sau:

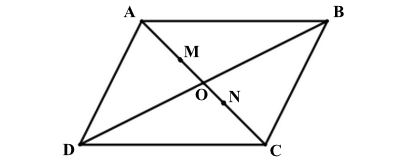a) Gọi M là trọng tâm ΔADB.

Khi đó ta có:

Vậy điểm M thỏa mãn  là trọng tâm của ΔADB.

b) Tương tự câu a)

Điểm N thỏa mãn  là trọng tâm của ΔDBC.

c) ABCD là hình bình hành có tâm O nên O là giao của hai đường chéo AC và BD, đồng thời là trung điểm của mỗi đường.

Khi đó AO là đường trung tuyến của tam giác ABD nên trọng tâm M của tam giác này nằm trên cạnh AO thỏa mãn AM = AO nên OM = AO.

Và CO là đường trung tuyến của tam giác BDC nên trọng tâm N của tam giác này nằm trên cạnh CO thỏa mãn CN = CO nên ON = CO.

Mà AO = CO.

Do đó: ON = OM.

Và O, M, N thẳng hàng (cùng thuộc đường chéo AC).

Nên O là trung điểm của MN.

Suy ra

Mà  nên điểm P trùng với điểm O.

Vậy điểm P thỏa mãn  là tâm O của hình bình hành ABCD.