Công thức Nhị thức Newton, Tam giác Pascal? Toán 10 chân trời tập 2 chương 8 bài 3

Công thức Nhị thức Newton, Tam giác Pascal, cách khai triển nhị thức Newton như thế nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Khai triển nhị thức Newton

– Hai công thức khai triển:

• (a + b)⁴ = C₄⁰ a⁴ + C₄¹ a³b +  C₄² a²b² +  C₄³ ab³ + C₄⁴ b⁴ 

= a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

• (a + b)⁵ = C₅⁰ a⁵ + C₅¹ a⁴b +  C₅² a³b² +  C₅³ a²b³ + C₅⁴ ab⁴ + C₅⁵ b⁵ 

= a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) (a + b)ⁿ ứng với n = 4 và n = 5.

2. Tam giác Pascal

– Các hệ số trong khai triển nhị thức Newton (a + b)ⁿ với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.

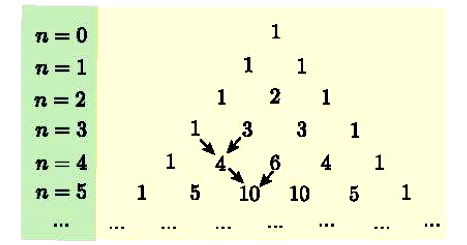
Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của 2 số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).

Bảng số trên được gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 – 1662).

* Ví dụ 1: Khai triển các biểu thức sau:

a) (x – 2)⁴;

b) (x + 2y)⁵.

* Lời giải:

a) Áp dụng khai triển nhị thức Newton với a = x và b = -2, ta có:

(x – 2)⁴ = C₄⁰ x⁴ + C₄¹ x³(–2) +  C₄² x²(–2)² +  C₄³ x(–2)³ + C₄⁴ (–2)⁴ 

= x⁴ – 8x³ + 24x² – 32x + 16.

Vậy (x – 2)⁴ = x⁴ – 8x³ + 24x² – 32x + 16.

b) Áp dụng khai triển nhị thức Newton với a = x và b = 2y, ta có:

(x + 2y)⁵ = C₅⁰ x⁵ + C₅¹ x⁴(2y) +  C₅² x³(2y)² +  C₅³ x²(2y)³ + C₅⁴ x(2y)⁴ + C₅⁵ (2y)⁵ 

= x⁵ + 10x⁴y + 40x³y² + 80x²y³ + 80xy⁴ + 32y.

Vậy (x + 2y)⁵ = x⁵ + 10x⁴y + 40x³y² + 80x²y³ + 80xy⁴ + 32y.

* Ví dụ 2: Sử dụng công thức nhị thức Newton, chứng tỏ rằng:

a) C₄⁰ + 2C₄¹  + 2²C₄² + 2³C₄³ + 2⁴C₄⁴ = 81

b) C₄⁰ – 2C₄¹  + 2²C₄² – 2³C₄³ + 2⁴C₄⁴ = 1

* Lời giải:

a) C₄⁰ + 2C₄¹  + 2²C₄² + 2³C₄³ + 2⁴C₄⁴ = 81

Ta có:

(1 + 2)⁴ = C₄⁰ 1⁴ + C₄¹ 1³.2 + C₄² 1².2² + C₄³ 1.2³ + C₄⁴ 2⁴

⇔ 3⁴ = C₄⁰ + 2C₄¹  + 2²C₄² + 2³C₄³ + 2⁴C₄⁴ 

⇔ C₄⁰ + 2C₄¹  + 2²C₄² + 2³C₄³ + 2⁴C₄⁴ = 81 (đpcm)

b) C₄⁰ – 2C₄¹  + 2²C₄² – 2³C₄³ + 2⁴C₄⁴ = 1

Ta có:

(1 – 2)⁴ = C₄⁰ 1⁴ + C₄¹ 1³.(–2) + C₄² 1².(–2)² + C₄³ 1.(–2)³ + C₄⁴ (–2)⁴

⇔ (–1)⁴ = C₄⁰ – 2C₄¹  + 2²C₄² – 2³C₄³ + 2⁴C₄⁴ 

⇔  C₄⁰ – 2C₄¹  + 2²C₄² – 2³C₄³ + 2⁴C₄⁴ = 1 (đpcm)