Định lí Côsin và Định lí Sin trong tam giác Hệ quả của định lí Sin và Côsin? Toán 10 chân trời tập 1 chương 4 bài 2

Định lí Côsin và Định lí Sin trong tam giác Hệ quả của định lí Sin và Côsin là gì? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Định lí côsin trong tam giác

Cho tam giác ABC

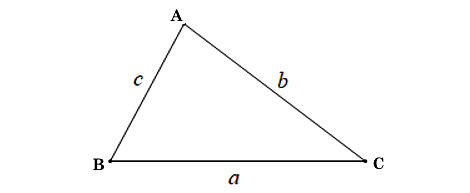
Định lí côsin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:

a² = b² + c² – 2bc.cosA;

b² = c² + a² – 2ca.cosB;

c² = a² + b² – 2ab.cosC.

• Hệ quả của định lí Côsin:

* Ví dụ: Tính các cạnh và các góc chưa biết của tam giác ABC trong Hình sau.

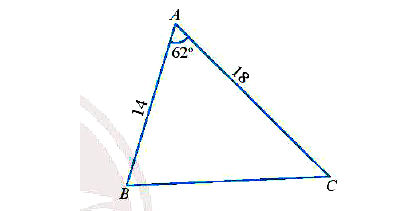
* Lời giải:

Áp dụng định lý côsin cho tam giác ABC ta có:

BC² =  AB² +  AC² – 2AB.AC.cosA   = 14² +  18² – 2.14.18. cos62° ≈ 283,4.

Suy ra BC ≈ 16,8.

Áp dụng hệ quả của định lí côsin ta có:

Mặt khác trong tam giác ABC ta có: 

Vậy BC ≈ 16,8; ∠B ≈ 71^o ; ∠C = 47^o 

2. Định lí sin trong tam giác

• Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:

trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.

Từ định lí sin, ta có hệ quả sau đây:

• Hệ quả của định lí Sin:

a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;

* Ví dụ: Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình sau.

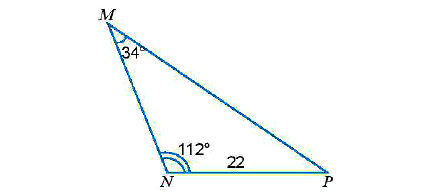
* Lời giải:

Trong tam giác MNP ta có: 

Vì  nên tam giác MNP cân tại N.

Do đó MN = NP = 22.

Áp dụng định lí sin cho tam giác MNP ta có :

Vậy các cạnh và các góc chưa biết của tam giác MNP là: ∠P = 34⁰;  MN = 22 ; MP ≈ 36,5.

3. Các công thức tính diện tích tam giác

Cho tam giác ABC. Ta kí hiệu:

+) BC = a, CA = b, AB = c.

+) h_a, h_b, h_c là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB.

+) R là bán kính đường tròn ngoại tiếp tam giác.

+) r là bán kính đường tròn nội tiếp tam giác.

+) p là nửa chu vi tam giác.

+) S là diện tích tam giác.

Ta có các công thức tính diện tích tam giác sau:

(1) S = (1/2).a.h_a = (1/2).b.h_b = (1/2).c.h_c

(2) S = (1/2).ab.sinC = (1/2).bc.sinA = (1/2).ac.sinB;

(3) S = abc/4R

(4) S = pr;

(5)  (Công thức Heron).

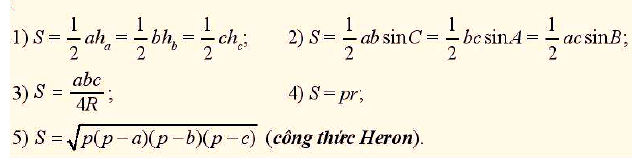
* Ví dụ: Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:

a) Các cạnh b = 14, c = 35 và 

b) Các cạnh a = 4, b = 5, c = 3.

* Lời giải:

a) Áp dụng công thức tính diện tích tam giác ABC ta có:

Vậy diện tích tam giác ABC là  212,2 (đơn vị diện tích).

Áp dụng định lí côsin cho tam giác ABC ta có:

a² = b² + c² – 2bccosA = 14² + 35² – 2.14.35.cos60° = 931

Áp dụng định lí sin ta có:

Vậy diện tích tam giác ABC là  212,2 (đơn vị diện tích), bán kính đường tròn ngoại tiếp tam giác ABC là 17,6 (đơn vị độ dài).

b) Ta có nửa chu vi của tam giác ABC là:  

Áp dụng công thức Heron ta có diện tích tam giác ABC là :

Mặt khác:  .

Vậy diện tích tam giác ABC là 6 (đơn vị diện tích), bán kính đường tròn ngoại tiếp tam giác ABC là 2,5 (đơn vị độ dài).