Hotline 0936685849

Giải tam giác là gì áp dụng giải tam giác trong thực tế? Toán 10 chân trời tập 1 chương 4 bài 3

10:25:0824/11/2023

Chào các em! Hôm nay chúng ta sẽ cùng tổng hợp lại những kiến thức quan trọng nhất trong Bài 3: Giải Tam Giác và Ứng Dụng Thực tế của chương trình Toán 10, bộ sách Chân trời sáng tạo. Bài viết này sẽ giúp các em củng cố lý thuyết về cách giải một tam giác và quan trọng hơn là thấy được cách áp dụng các định lý sin, cosin vào việc giải quyết các bài toán thực tiễn trong cuộc sống.

1. Giải tam giác

• Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó.

Để giải tam giác, ta thường sử dụng một cách hợp lí các hệ thức lượng như: định lí sin, định lí côsin và các công thức tính diện tích tam giác.

* Ví dụ: Giải tam giác ABC biết AB = 45, AC = 32 và $\small \widehat{A}$ = 60^o

* Lời giải:

+ Theo định lí côsin ta có:

BC² = AB² + AC² – 2.AB.AC.cosA

⇒ BC² = 45² + 32² – 2.45.32.cos60° = 1609.

⇒ BC ≈ 40,11.

+) Theo định lí sin ta có:

$\small \frac{BC}{sinA}=\frac{AC}{sinB}\Rightarrow \frac{40,11}{sin60^0}=\frac{32}{sinB}$

$\small \Rightarrow sinB=\frac{32.sin60^0}{40,11}\approx 0,69$

⇒ $\small \widehat{B}=44^0$ (không thể xảy ra trường hợp $\small \widehat{B}=136^0$ vì khi đó $\small \widehat{A}+\widehat{B}$ > 180^o)

Xét tam giác ABC có $\small \widehat{A}$ = 60^o, $\small \widehat{B}$ = 44^o ta có:

$\small \widehat{A}+\widehat{B}+\widehat{C}=180^0$ (định lí tổng ba góc trong tam giác)

$\small \Rightarrow \widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-44^0=76^0$

Vậy BC ≈ 40,11; ∠B ≈ 44^o và ∠C ≈ 76^o

2. Áp dụng giải tam giác vào thực tế

Vận dụng giải tam giác giúp ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.

* Ví dụ 1: Một đường hầm dự kiến xây dựng xuyên qua một ngọn núi. Để ước tính chiều dài của đường hầm, một kĩ sư đã thực hiện các phép đo và cho ra kết quả như Hình 1. Tính chiều dài của đường hầm từ các số liệu đã khảo sát được.

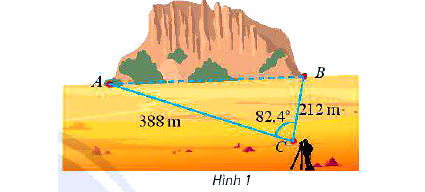
Áp dụng giải tam giác trong thực tế

* Lời giải:

Áp dụng định lí cosin trong tam giác ABC, ta có:

AB² = CA² + CB² – 2.CA.CB.cosC = 388² + 212² – 2.388.212.cos82,4⁰ ≈ 173730

Suy ra: AB ≈ 417 (m)

Vậy đường hàm dài khoảng 417 (m)

* Ví dụ 2: Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với vận tốc 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc 25° về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilômét? Giả sử chúng đang ở cùng độ cao.

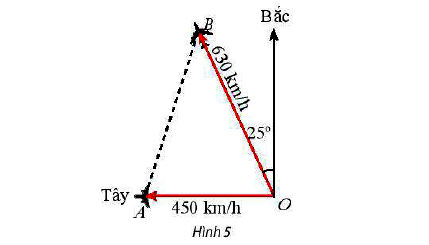Áp dụng giải tam giác trong thực tế * Lời giải:

Gọi A và B lần lượt là vị trí của hai máy bay sau khi cất cánh 90 phút.

Đổi 90 phút = 1,5 giờ.

Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng tây đi được quãng đường là: 450.1,5 = 675 km, tức là OA = 675 km.

Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng lệch bắc 25° về phía tây đi được quãng đường là: 630.1,5 = 945 km, tức là OB = 945 km.

Ta có: $\small \widehat{AOB}=90^0-25^0=65^0$

Áp dụng định lí côsin cho tam giác OAB ta có:

AB² = OA² + OB² – 2.OA.OB.cos $\small \widehat{AOB}$ = 675² + 945² – 2.675.945.cos65^o ≈ 809 494,8

Suy ra: AB ≈ 899,7

Vậy sau 90 phút hai máy bay cách nhau khoảng 899,7 km.

Qua bài học này, các em đã thấy được sức mạnh của toán học trong việc giải quyết các vấn đề thực tế. Bằng cách áp dụng một cách linh hoạt định lý sin, định lý cosin, chúng ta có thể dễ dàng tính toán các đại lượng còn thiếu trong tam giác. Nắm vững kỹ năng giải tam giác sẽ là nền tảng vững chắc để các em học tốt các chương trình hình học sau này và áp dụng vào nhiều lĩnh vực khác của cuộc sống.

• Xem thêm:

Lý thuyết Toán 10 bài 1 chương 4 Chân trời sáng tạo

Lý thuyết Toán 10 bài 2 chương 4 Chân trời sáng tạo