Hàm số đồng biến nghịch biến khi nào, tập xác định và tập giá trị của hàm số, đồ thị hàm số? Toán 10 chân trời tập 1 chương 3 bài 1

Hàm số đồng biến nghịch biến khi nào, tập xác định và tập giá trị của hàm số là gì, đồ thì hàm số như thế nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Hàm số. Tập xác định và tập giá trị của hàm số

– Giả sử x và y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số D.

Nếu với mỗi giá trị x thuộc D, ta xác định được một và chỉ một giá trị tương ứng y thuộc tập hợp số thực ℝ thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D được gọi là tập xác định của hàm số.

Tập hợp T gồm tất cả các giá trị y (tương ứng với x thuộc D) gọi là tập giá trị của hàm số.

* Chú ý:

+ Ta thường dùng kí hiệu f(x) để chỉ giá trị y tương ứng với x, nên hàm số còn được viết là y = f(x).

+ Một hàm số có thể đượ cho bằng bảng, bằng biểu đồ hoặc bằng công thức như đã học ở cấp Trung học cơ sở.

+ Khi một hàm số được cho bằng công thức mà không chỉ rõ tập xác định thì ta quy ước:

Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

+ Một hàm số có thể được cho bởi hai hay nhiều công thức.

* Ví dụ 1: Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:

Vì sao bảng này biểu thị một hàm số ? Tìm tập xác định của hàm số này.

* Lời giải:

Dựa vào bảng ta thấy, với mỗi một mốc thời gian (t) ta xác định được một và chỉ một giá trị tương ứng của vận tốc (v). Do đó v là hàm số của t.

Tập xác định của hàm số là: D = {0,5; 1; 1,2; 1,8; 2,5}.

* Ví dụ 2: Tìm tập xác định của các hàm số sau:

a) 

b) 

* Lời giải:

a) 

Biểu thức f(x) có nghĩa nếu và chỉ nếu 2x + 7 ≥ 0

⇔ 2x ≥ –7

⇔ x ≥ –7/2

Vậy tập xác định của hàm số này là D = [–7/2; +∞)

b) 

Biểu thức f(x) có nghĩa nếu và chỉ nếu: x² – 3x + 2 ≠ 0

⇔ (x – 2)(x – 1) ≠ 0

⇔ (x – 2) ≠ 0 và (x – 1) ≠ 0

⇔ x ≠ 2 và x ≠ 1

Vậy tập xác định của hàm số này là D = ℝ\{1; 2}.

2. Đồ thị hàm số

– Cho hàm số y = f(x) có tập xác định D.

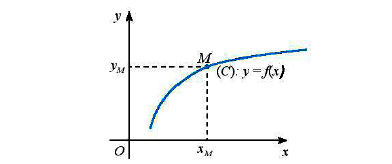
Trên mặt phẳng tọa độ Oxy, đồ thị (C) của hàm số là tập hợp tất cả các điểm M(x; y) với x ∈ D và y = f(x).

Vậy (C) = {M(x; f(x)| x ∈ D}.

* Chú ý: Điểm M(x_M; y_M) thuộc đồ thị hàm số y = f(x) khi và chỉ khi x_M ∈ D và y_M = f(x_M).

* Ví dụ: Vẽ đồ thị hàm số f(x) = 3x + 8

* Lời giải:

Hàm số y = f(x) = 3x + 8 có tập xác định D = ℝ

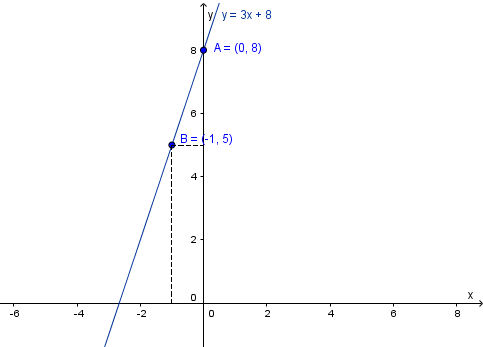
Với x = 0 thì y = f(0) = 3.0 + 8 = 8, ta được điểm A(0; 8).

Với x = –1 thì y = f(–1) = 3.(–1) + 8 = 5, ta được điểm B(–1; 5).

Đồ thị hàm số f(x) = 3x + 8 là đường thẳng đi qua các điểm A(0; 8) và B(–1;5).

3. Hàm số đồng biến, hàm số nghịch biến

– Với hàm số y = f(x) xác định trên khoảng (a; b), ta nói:

+ Hàm số đồng biến trên khoảng (a; b) nếu

∀x₁, x₂ ∈ (a; b), x₁ < x₂ ⇒ f(x₁) < f(x₂).

+ Hàm số nghịch biến trên khoảng (a; b) nếu

∀x₁, x₂ ∈ (a; b), x₁ < x₂ ⇒ f(x₁) > f(x₂).

* Nhận xét:

+ Khi hàm số đồng biến (tăng) trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải. Ngược lại, khi hàm số nghịch biến (giảm) trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.

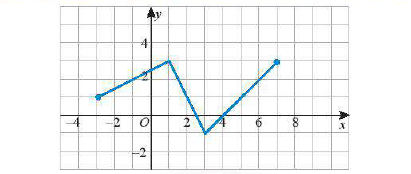
* Ví dụ: Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:

* Lời giải:

Tập xác định của hàm số là D = [–3; 7].

Quan sát trên đồ thị hàm số, ta thấy:

Trên khoảng (–3; 1) đồ thị của hàm số đi lên từ trái sang phải. Do đó hàm số đồng biến trên khoảng (-3; 1).

Trên khoảng (1; 3) đồ thị của hàm số đi xuống từ trái sang phải. Do đó hàm số nghịch biến trên khoảng (1; 3).

Trên khoảng (3; 7) đồ thị của hàm số đi lên từ trái sang phải. Do đó hàm số đồng biến trên khoảng (3; 7).

Vậy hàm số đồng biến trên khoảng (–3; 1) và (3; 7); nghịch biến trên khoảng (1; 3).