Công thức tính phương sai và độ lệch chuẩn, ý nghĩa của phương sai, độ lệch chuẩn? Toán 10 chân trời tập 1 chương 6 bài 4

Công thức tính phương sai và độ lệch chuẩn, ý nghĩa của phương sai, độ lệch chuẩn như thế nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Khoảng biến thiên và khoảng tứ phân vị

1.1. Khoảng biến thiên và khoảng tứ phân vị

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

x₁ ≤ x₂ ≤ … ≤ x_n.

• Khoảng biến thiên của một mẫu số liệu, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó, tức là:

R = x_n – x₁.

• Khoảng tứ phân vị, kí hiệu là ∆_Q, là hiệu giữa Q_3­ và Q₁, tức là:

∆_Q = Q₃ – Q₁.

* Ví dụ: Hãy tính khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu:

10; 3; 5; 7; 20; 1; 4; 9.

* Lời giải:

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được: 1; 3; 4; 5; 7; 9; 10; 20.

- Khoảng biến thiên của mẫu số liệu là R = 20 – 1 = 19.

- Cỡ mẫu là n = 8, là số chẵn nên giá trị tứ phân vị thứ hai là:

Q₂ =  (7 + 9) = 6.

- Tứ phân vị thứ nhất là trung vị của mẫu: 10; 3; 5; 7.

Do đó Q₁ = (3 + 5) = 4.

- Tứ phân vị thứ 3 là trung vị của mẫu: 7; 9; 10; 20.

Do đó Q₃ =  (9 + 10) = 9,5.

- Khoảng tứ phân vị của mẫu là: ∆_Q = 9,5 – 4 = 5,5.

1.2. Ý nghĩa của khoảng biến thiên và khoảng tứ phân vị:

Khoảng biến thiên đặc trưng cho độ phân tán của toàn bộ mẫu số liệu.

Khoảng tứ phân vị đặc trưng cho độ phân tán của một nửa các số liệu, có giá trị thuộc đoạn từ Q₁ đến Q₃ trong mẫu.

Khoảng tứ phân vị không bị ảnh hưởng bởi các giá trị rất lớn hoặc rất bé trong mẫu.

* Ví dụ: Dưới đây là bảng số liệu thống kê của Biểu đồ nhiệt độ trung bình các tháng trong năm 2019 của hai tỉnh Lai Châu và Lâm Đồng (được đề cập đến ở hoạt động khởi động của bài học).

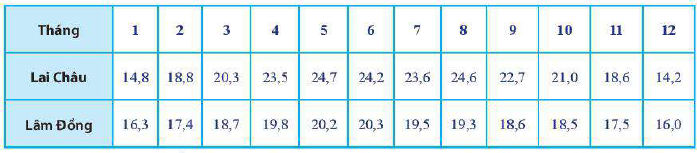
a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm Đồng.

b) Hãy cho biết trong một năm, nhiệt độ ở địa phương nào ít thay đổi hơn.

* Lời giải:

a) Tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm Đồng.

* Tỉnh Lai Châu:

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

14,2; 14,8; 18,6; 18,8; 20,3; 21,0; 22,7; 23,5; 23,6; 24,2; 24,6; 24,7.

+ Khoảng biến thiên của mẫu số liệu là: R = 24,7 – 14,2 = 10,5.

+ Cỡ mẫu là n = 12 là số chẵn nên giá trị tứ phân vị thứ hai là:

Q₂ = (21,0 + 22,7) = 21,85.

+ Tứ phân vị thứ nhất là trung vị của mẫu: 14,2; 14,8; 18,6; 18,8; 20,3; 21,0.

Do đó Q₁ = (18,6 + 18,8) = 18,7.

+ Tứ phân vị thứ ba là trung vị của mẫu: 22,7; 23,5; 23,6; 24,2; 24,6; 24,7.

Do đó Q₃ = (23,6 + 24,2) = 23,9.

+ Khoảng tứ phân vị của mẫu là: ∆_Q = 23,9 – 18,7 = 5,2.

* Tỉnh Lâm Đồng:

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

16,0; 16,3; 17,4; 17,5; 18,5; 18,6; 18,7; 19,3; 19,5; 19,8; 20,2; 20,3.

+ Khoảng biến thiên của mẫu số liệu là: R' = 20,3 – 16,0 = 4,3.

+ Cỡ mẫu là n = 12 là số chẵn nên giá trị tứ phân vị thứ hai là:

Q'₂ = (18,6 + 18,7) = 18,65.

+ Tứ phân vị thứ nhất là trung vị của mẫu: 16,0; 16,3; 17,4; 17,5; 18,5; 18,6.

Do đó Q'₁ = (17,4 + 17,5) = 17,45.

+ Tứ phân vị thứ ba là trung vị của mẫu: 18,7; 19,3; 19,5; 19,8; 20,2; 20,3.

Do đó Q'₃ = (19,5 + 19,8) = 19,65.

+ Khoảng tứ phân vị của mẫu là: ∆'_Q = 19,65 – 17,45 = 2,2.

b) Xét về cả khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của cả hai tỉnh, ta thấy: 10,5 > 4,3 hay R > R' và 5,2 > 2,2 hay ∆_Q > ∆'_Q.

Điều đó có nghĩa là trong một năm, nhiệt độ ở Lâm Đồng ít thay đổi hơn.

1.3. Giá trị ngoại lệ

Khoảng tứ phân vị được dùng để xác định các giá trị ngoại lệ trong mẫu, đó là các giá trị quá nhỏ hay quá lớn so với đa số các giá trị của mẫu. Cụ thể, phần tử x trong mẫu là giá trị ngoại lệ nếu x > Q₃ + 1,5∆_Q hoặc x < Q₁ – 1,5∆_Q.

Sự xuất hiện của các giá trị ngoại lệ làm cho số trung bình và phạm vi của mẫu thay đổi lớn. Do đó, khi mẫu có giá trị ngoại lệ, người ta thường sử dụng trung vị và khoảng tứ phân vị để đo mức độ tập trung và mức độ phân tán của đa số các phần tử trong mẫu số liệu.

* Ví dụ: Trong ví dụ ở phần 1.1, ta có:

Q₁ – 1,5∆_Q = 4 – 1,5 . 5,5 = – 4,25;

Q₃ + 1,5∆_Q = 9,5 + 1,5 . 5,5 = 17,75.

Do đó, mẫu có một giá trị ngoại lệ là 20.

2. Phương sai và độ lệch chuẩn

2.1. Công thức tính phương sai và độ lệch chuẩn

* Giả sử ta có một mẫu số liệu là x₁, x₂, …, x_n.

• Phương sai của mẫu số liệu này, kí hiệu là S², được tính bởi công thức:

trong đó  là số trung bình của mẫu số liệu.

• Căn bậc hai của phương sai được gọi là độ lệch chuẩn, kí hiệu là S.

* Chú ý: Có thể biến đổi công thức tính phương sai ở trên thành:

Trong thống kê, người ta cũng quan tâm đến phương sai hiệu chỉnh, kí hiệu là  , được tính bởi công thức:

* Giả sử mẫu số liệu được cho dưới dạng bảng tần số:

Khi đó, công thức tính phương sai trở thành:

trong đó n = n₁ + n₂ + … + n_k.

Có thể biến đổi công thức tính phương sai trên thành:

* Ví dụ: Điều tra số con của mỗi hộ gia đình trong tổ dân cư xóm 2, kết quả được ghi lại ở bảng sau:

Tính phương sai và độ lệch chuẩn của mẫu số liệu.

* Lời giải:

Tổng số hộ gia đình là: n = 4 + 4 + 8 + 3 + 1 = 20 (hộ gia đình).

Số trung bình của mẫu số liệu trên là

Phương sai của mẫu số liệu trên là:

Độ lệch chuẩn của mẫu số liệu trên là:

2.2. Ý nghĩa của phương sai và độ lệch chuẩn

Phương sai là trung bình cộng của các bình phương độ lệch từ mỗi giá trị của mẫu số liệu đến số trung bình.

Phương sai và độ lệch chuẩn được dùng để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình. Phương sai và độ lệch chuẩn càng lớn thì các giá trị của mẫu càng cách xa nhau (có độ phân tán lớn).

* Ví dụ: Bảng dưới đây thống kê tổng số giờ nắng trong năm 2019 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở Tuyên Quang và Cà Mau.

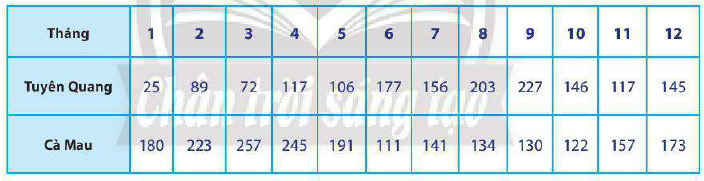
a) Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh.

b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh.

* Lời giải:

a) Tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh.

* Tỉnh Tuyên Quang:

+ Số trung bình:

 = (25 + 89 + 72 + 117 + 106 + 177 + 156 + 203 + 227 + 146 + 117 + 145)/12 ≈ 131,67

+ Phương sai mẫu số liệu ở tỉnh Tuyên Quang là:

 = (25² + 89² + 72² + 117² + 106² + 177² + 156² + 203² + 227² + 146² + 117² + 145²)/12 ≈ 2920,34

+ Độ lệch chuẩn mẫu số liệu ở tỉnh Tuyên Quang là:

* Tỉnh Cà Mau:

+ Số trung bình:

= (180 + 223 + 257 + 245 + 191 + 111 + 141 + 134 + 130 + 122 + 157 + 173)/12 = 172

+ Phương sai mẫu số liệu ở tỉnh Cà Mau là:

= (180² + 223² + 257² + 245² + 191² + 111² + 141² + 134² + 130² + 122² + 157² + 173²)/12 = 2183

+ Độ lệch chuẩn mẫu số liệu ở tỉnh Cà Mau là:

b) Phương sai mẫu và độ lệch chuẩn mẫu số liệu ở tỉnh Tuyên Quang cao hơn tỉnh Cà Mau nên tổng số giờ nắng trong năm 2019 theo từng tháng ở tỉnh Tuyên Quang có độ phân tán cao hơn ở tỉnh Cà Mau.

Do đó, sự thay đổi tổng số giờ nắng theo từng tháng ở tỉnh Cà Mau ổn định (có ít sự thay đổi) hơn so với tỉnh Tuyên Quang.