Khái niệm hệ Bất phương trình bậc nhất hai ẩn, cách biểu diễn miền nghiệm của hệ bất phương trình? Toán 10 chân trời tập 1 chương 2 bài 2

Khái niệm Hệ bất phương trình bậc nhất hai ẩn, cách biểu diễn miền nghiệm của hệ bất phương trình  bậc nhất 2 ẩn và cách tìm giá trị lớn nhất hay nhỏ nhất của biểu thức F = ax + b trên một miền đa giác như nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Khái niệm hệ bất phương trình bậc nhất hai ẩn

• Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.

• Trên mặt phẳng tọa độ Oxy, tập hợp các điểm (x₀; y₀) có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trình đó.

* Ví dụ 1:

Hệ bất phương trình:  

là một hệ bất phương trình hai ẩn x, y gồm hai bất phương trình 3x + y – 2 ≤ 0 và 2x – y + 1 ≥ 0 đều là bất phương trình bậc nhất hai ẩn x, y.

Hệ bất phương trình:  

không phải là hệ bất phương trình bậc nhất hai ẩn bởi bất phương trình x² + 2y² < 3 không phải bất phương trình bậc nhất hai ẩn do chứa x², y².

* Ví dụ 2: Cho hệ bất phương trình hai ẩn 

Cặp số (x; y) = (0; 1) có là nghiệm của hệ bất phương trình trên không?

* Lời giải:

Thay x = 0 và y = 1 vào bất phương trình 3x + y – 2 ≤ 0 ta có: 0 + 1 – 2 = –1 < 0 là mệnh đề đúng nên cặp số (x; y) = (0; 1) là nghiệm của bất phương trình 3x + y – 2 ≤ 0.

Thay x = 0 và y = 1 vào bất phương trình 2x – y + 1 ≥ 0 ta có: 0  – 1 + 1 = 0  ≥ 0 là mệnh đề đúng nên cặp số (x; y) = (0; 1) là nghiệm của bất phương trình 2x – y + 1 ≥ 0.

Cặp (x; y) = (0; 1)  là nghiệm của bất phương trình 3x + y – 2 ≤ 0  và cũng là nghiệm của bất phương trình 2x – y + 1 ≥ 0.

Do đó cặp số (x; y) = (0; 1) là nghiệm của hệ bất phương trình đã cho.

2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn

Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ Oxy, ta thực hiện như sau:

– Trên cùng mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ.

– Phần giao của các miền nghiệm là miền nghiệm của hệ bất phương trình.

* Chú ý: Miền mặt phẳng tọa độ bao gồm một đa giác lồi và phần nằm bên trong đa giác đó được gọi là một miền đa giác.

* Ví dụ: Biểu diễn miền nghiệm của hệ bất phương trình:

* Lời giải:

Biểu diễn miền nghiệm của từng bất phương trình trên mặt phẳng Oxy.

- Xác định miền nghiệm D₁ của bất phương trình x + y ≤ 8:

Lấy điểm O(0; 0) không thuộc đường thẳng d₁: x + y = 8, ta có: 0 + 0 = 0 < 8. Do đó miền nghiệm của bất phương trình x + y ≤ 8 là nửa mặt phẳng bờ là đường thẳng d (kể cả đường thẳng d₁) và chứa gốc tọa độ O.

- Xác định miền nghiệm D₂ của bất phương trình 2x +3y ≤ 18:

Lấy điểm O(0; 0) không thuộc đường thẳng d₂: 2x + 3y = 18, ta có: 2.0 + 3.0 = 0 < 18. Do đó miền nghiệm của bất phương trình 2x +3y ≤ 18 là nửa mặt phẳng bờ là đường thẳng d₂ (kể cả đường thẳng d₂) và chứa gốc tọa độ O.

- Xác định miền nghiệm D₃ của bất phương trình x ≥ 0:

Miền nghiệm của bất phương trình x ≥ 0  là nửa mặt phẳng bên phải trục Oy và kể cả bờ Oy.

- Xác định miền nghiệm D₄ của bất phương trình y ≥ 0:

 Miền nghiệm của bất phương trình y ≥ 0  là nửa mặt phẳng bên trên trục Ox và kể cả bờ Ox.

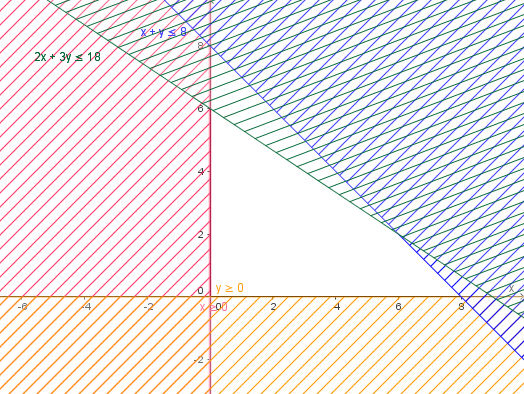
Kết quả ta được miền nghiệm là phần không bị gạch chéo ở hình trên.

3. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác

• Hệ bất phương trình giúp ta mô tả được nhiều bài toán thực tế để tìm ra cách giải quyết tối ưu. Chúng thường được đưa về bài toán tìm giá trị lớn nhất (GTLN) hoặc giá trị nhỏ nhất (GTNN) của biểu thức F = ax + by trên một miền đa giác.

• Người ta chứng minh được F = ax + by đạt giá trị lớn nhất hoặc nhỏ nhất tại một trong các đỉnh của đa giác

* Ví dụ: Bạn Vinh cần phải làm bài tập trong vòng không quá 2 giờ để nộp. Mỗi bài toán cần 10 phút để làm xong, mỗi bài Vật lí cần 20 phút để làm xong. Gọi x, y lần lượt là số bài tập Toán, Vật lí bạn Vinh sẽ làm được. Lập hệ bất phương trình mô tả điều kiện của x và y và biểu diễn miền nghiệm của hệ đó. Số bài nhiều nhất mà bạn Vinh có thể làm được là bao nhiêu?

* Lời giải:

Số phút bạn Vinh làm xong x bài Toán là: 10x (phút).

Số phút bạn Vinh làm xong y bài Vật lí là: 20y (phút).

Tổng số phút để Vinh làm x bài toán và y bài lí là: 10x + 20y (phút).

Vì bạn Vinh cần phải làm bài tập trong vòng không quá 2 giờ = 120 phút nên ta có:

10x + 20y ≤ 120 hay x + 2y ≤ 12.

Số bài tập bạn Vinh làm luôn không âm nên x ≥ 0, y ≥ 0.

Ta có hệ bất phương trình sau: 

Biểu diễn miền nghiệm của hệ bất phương trình:

– Xác định miền nghiệm D₁ của bất phương trình x ≥ 0.

+ Đường thẳng x = 0 là trục tọa độ Oy.

+ Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy (kể cả trục Oy) nằm bên phải trục Oy.

– Tương tự, miền nghiệm D₂ của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox (kể cả trục Ox) nằm bên trên trục Ox.

– Miền nghiệm D₃ của bất phương trình x + 2y ≤ 12 $\iff$ x + 2y – 12 ≤ 0.

+ Vẽ đường thẳng ∆: x + 2y – 12 = 0.

Đường thẳng ∆ đi qua hai điểm A(0; 6) và B(12; 0).

+ Xét gốc toạ độ O(0; 0) có: 0 + 2. 0 – 12 = – 12 ≤ 0 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + 2y – 12 ≤ 0.

Do đó, miền nghiệm D₃ của bất phương trình x + 2y ≤ 12 là nửa mặt phẳng bờ ∆ (kể cả bờ ∆) chứa gốc tọa độ O.

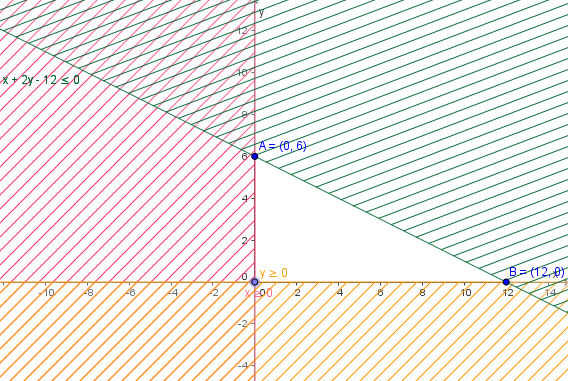
Miền nghiệm (miền không bị gạch) của hệ bất phương trình trên là miền tam giác OAB với: O(0; 0), A(0; 6), B(12; 0).

Số bài mà bạn Vinh làm được là: F(x; y) = x + y.

Tại O(0; 0): F = 0 + 0 = 0;

Tại A(0; 6): F = 0 + 6 = 6;

Tại B(12; 0): F = 12 + 0 = 12;

Do đó giá trị lớn nhất của F(x; y) bằng 12 khi (x; y) = (12; 0).

Vậy bạn Vinh làm được nhiều nhất là 12 bài khi làm 12 bài Toán và không làm bài tập Vật lí.