Hàm số bậc hai là gì, cách vẽ đồ thị hàm số bậc 2 và sự biến thiên của hàm số bậc hai? Toán 10 chân trời tập 1 chương 3 bài 2

Hàm số bậc hai là gì, cách vẽ đồ thị hàm số bậc 2 và sự biến thiên của hàm số bậc hai như nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Hàm số bậc hai

– Hàm số bậc hai theo biến x là hàm số cho bởi công thức có dạng y = f(x) = ax² + bx + c với a, b, c là các số thực và a khác 0.

– Tập xác định của hàm số bậc hai là ℝ.

* Ví dụ:

• y = 2x² + 5x + 1 là hàm số bậc hai vì hàm số này được cho bởi công thức có dạng y = f(x) = ax² + bx + c với a = 2 ≠ 0, b = 5, c = 1.

• y = 3x³ + 2x ‒ 5 không phải là hàm số bậc hai bởi hàm số này có chứa x³, không được cho bởi công thức dạng y = f(x) = ax² + bx + c.

2. Đồ thị hàm số bậc hai

• Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax² + bx + c (với a ≠ 0) là một parabol (P):

+ Có đỉnh S với hoành độ , tung độ  với Δ = b² – 4ac.

+ Có trục đối xứng là đường thẳng x = –b/2a (đường thẳng này đi qua đỉnh S và song song với trục Oy nếu b ≠ 0, trùng với trục Oy nếu b = 0);

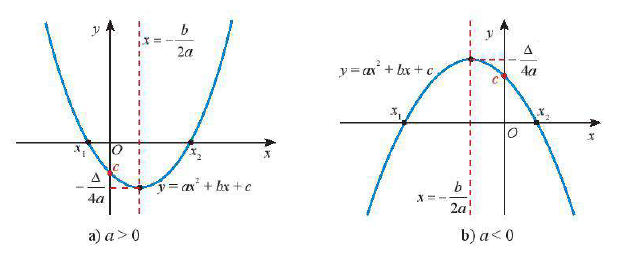
+ Bề lõm quay lên trên nếu a > 0, quay xuống dưới nếu a < 0;

+ Cắt trục tung tại điểm có tung độ bằng c, tức là đồ thị đi qua điểm có tọa độ (0; c).

* Chú ý:

+ Nếu b = 2b’ thì (P) có đỉnh S(–b'/a; –Δ/a)

+ Nếu phương trình ax² + bx + c = 0 có hai nghiệm x₁; x₂ thì đồ thị hàm số bậc hai y = ax² + bx + c cắt trục hoành tại hai điểm lần lượt có hoành độ là hai nghiệm này (hình dưới).

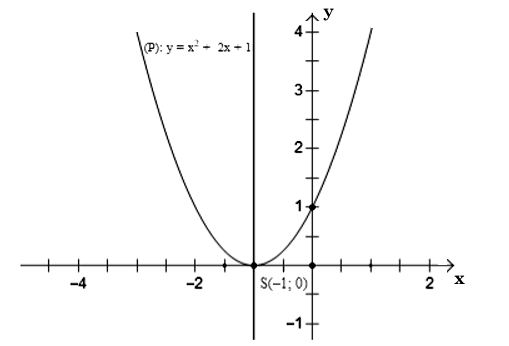
* Ví dụ: Cho hàm số bậc hai y = x² + 2x + 1.

Ta xác định a = 1; b = 2; c = 1; Δ = b² – 4ac = 0.

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = x² + 2x + 1 là một parabol (P):

+ Có đỉnh S với hoành độ x_S = –b/a = –1; tung độ y_S = –Δ/4a = 0

+ Có trục đối xứng d là đường thẳng x = ‒1 (đường thẳng này đi qua đỉnh S(‒1; 0) và song song với trục Oy);

+ Bề lõm của parabol quay lên trên do a = 1 > 0;

+ Cắt trục tung tại điểm có tung độ bằng 1, tức là đồ thị đi qua điểm có toạ độ (0; 1).

Đối với hàm số bậc hai y = x² + 2x + 1 ta thấy hệ số b = 2 là số chẵn nên cũng có thể tìm toạ độ đỉnh S(–b'/a; –Δ/a) với a = 1, b' = 1, c = 1 và Δ' = b'² – ac = 0.

Khi đó ta cũng tìm được S(‒1; 0).

* Cách vẽ đồ thị hàm số bậc hai:

Cách vẽ đồ thị hàm số bậc hai y = ax² + bx + c (với a ≠ 0):

(1) Xác định tọa độ đỉnh 

(2) Vẽ trục đối xứng d là đường thẳng 

(3) Tìm tọa độ giao điểm của đồ thị với trục tung (điểm A(0; c)) và giao điểm của đồ thị với trục hoành (nếu có).

Xác định thêm điểm đối xứng với A qua trục đối xứng d, là điểm 

(4) Vẽ parabol có đỉnh S, có trục đối xứng d, đi qua các điểm tìm được.

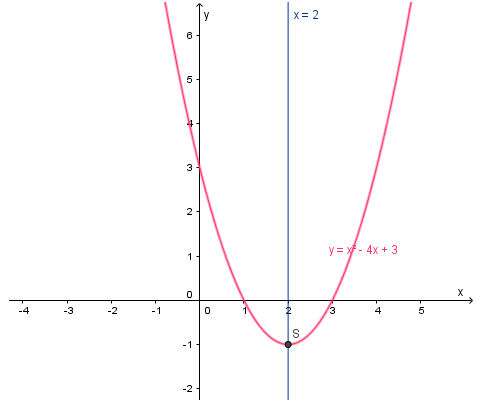
* Ví dụ: Vẽ đồ thị hàm số y = x² – 4x + 3.

* Lời giải:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) =  x² – 4x + 3 là một parabol (P):

- Có đỉnh S với hoàng độ x_S = 2, tung độ y_S = –1;

- Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

- Bề lõm quay lên trên vì a = 1 > 0;

- Cắt trục tung tại điểm có tung độ y = 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

3. Sự biến thiên của hàm số bậc hai

– Dựa vào đồ thị hàm số bậc hai y = ax² + bx + c (với a ≠ 0), ta có bảng tóm tắt về sự biến thiên của hàm số này như sau:

* Chú ý: Từ bảng biến thiên của hàm số bậc hai, ta thấy:

– Khi a > 0, hàm số đạt giá trị nhỏ nhất bằng –Δ/4a tại x = –b/2a và hàm số có tập giá trị là: [–Δ/4a; +∞)

– Khi a < 0, hàm số đạt giá trị lớn nhất bằng –Δ/4a tại x = –b/2avà hàm số có tập giá trị là T = (–∞; –Δ/4a]

* Ví dụ: Lập bảng biến thiên của hàm số y = –x² + 4x – 3. Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.

* Lời giải:

Đỉnh S có toạ độ:

y_S = –2² + 4.2 – 3 = 1

Vậy S(2; 1)

Vì hàm số bậc hai có a = –1 < 0 nên ta có bảng biến thiên sau.

Hàm số đạt giá trị lớn nhât bằng 1 khi x = 2.

4. Ứng dụng của hàm số bậc hai

Tầm bay cao và bay xa

Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên.

Trong mặt phẳng tọa độ Oxy, chọn điểm có tọa độ (0; y₀) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là:

Trong đó:

• g là gia tốc trọng trường (thường được chọn là 9,8 m/s²);

• α là góc phát cầu (so với phương ngang của mặt đất);

• v₀ là vận tốc ban đầu của cầu;

• y₀ là khoảng cách từ vị trí phát cầu đến mặt đất.

Đây là một hàm số bậc hai nên quỹ đạo chuyển động của cầu lông là một parabol.

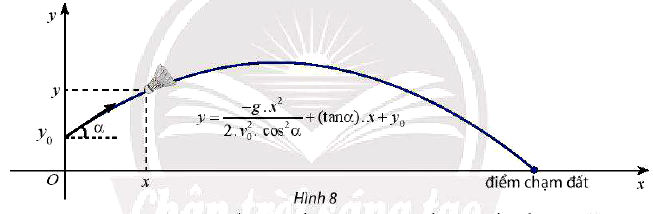
Xét trường hợp lặng gió, với vận tốc ban đầu và góc phát cầu đã biết, cầu chuyển động theo quỹ đạo parabol nên sẽ:

– Đạt vị trí cao nhất tại đỉnh parabol, gọi là tầm bay cao;

– Rơi chạm đất ở vị trí cách nơi đứng phát cầu một khoảng, gọi là tầm bay xa.

* Ví dụ: Một người đang tập chơi cầu lông có khuynh hướng phát cầu với góc 30 độ so với mặt đất.

a) Hãy tính khoảng cách từ vị trí người phát cầu đến vị trí cầu chạm đất, biết cầu rời vợt ở độ cao 0,7 m so với mặt đất và vận tốc ban đầu của cầu là 8 m/s (bỏ qua sức cản của gió và quỹ đạo của cầu trong mặt phẳng thẳng đứng, gia tốc trọng trường là 9,8 m/s²).

b) Giả thiết như câu a) và cho biết khoảng cách từ vị trí phát cầu đến lưới là 4 m. Lần phát cầu này có hỏng không? Cho biết mép trên của lưới cách mặt đất 1,524 m.

* Lời giải:

Chọn hệ trục tọa độ với vị trị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung.

Với g = 9,8 m/s², góc phát cầu α = 30°, vận tốc ban đầu của cầu là v₀ = 8 m/s, phương trình quỹ đạo của cầu là:

 (với x ≥ 0)

Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên y = 0.

Nên:

Giải phương trình này ta được: x ≈ –1,03 (không thoả) và x₂ ≈ 6,68 (thoả mãn)

Giá trị nghiệm cho ta khoảng cách từ vị trí người chơi đến vị trí cầu rơi chạm đất là 6,68 m.

b) Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biên phía bên sân đối phương thì lần phát cầu mới được xem là hợp lệ.

Ta cần so sánh tung độ của điểm trên quỹ đạo (có hoành độ bằng khoảng cách từ gốc tọa độ đến chân lưới phân cách) với chiều cao mép trên của lưới để tìm câu trả lời.

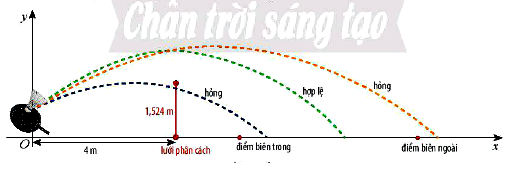
Khi x = 4, ta có: 

Suy ra: y < 1,524

Như vậy, lần phát cầu đã bị hỏng vì điểm trên quỹ đạo của cầu thấp hơn mép trên của lưới.