Giải bài 1 trang 96 Toán 6 Tập 1 SGK Cánh Diều

Đề bài:

Cho lục giác đều ABCDEG.

Các đường chéo chính AD, BE, CG, cắt nhau tại O (Hình 9).

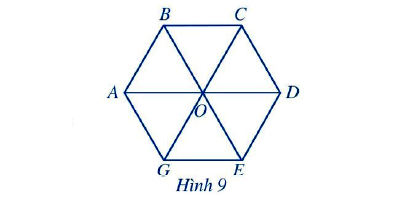
Vì sao OA = OB = OC = OD = OE = OG?

Phân Tích và Hướng Dẫn Giải:

Để giải thích tại sao các đoạn thẳng nối từ tâm đến các đỉnh lại bằng nhau, các em cần nhớ lại các đặc điểm của một lục giác đều:

1. Sáu cạnh bằng nhau: $AB=BC=CD=DE=EG=GA$.

2. Sáu góc bằng nhau.

3. Các đường chéo chính: Các đường chéo chính (nối các đỉnh đối diện) bằng nhau và cắt nhau tại một điểm duy nhất, gọi là tâm đối xứng O.

4. Khi các đường chéo chính cắt nhau tại O, chúng tạo thành sáu tam giác nhỏ có chung đỉnh O.

Ta sẽ chứng minh các tam giác này là tam giác đều, từ đó suy ra các cạnh của chúng bằng nhau.

Lời giải chi tiết:

Vì ABCDEG là lục giác đều nên:

Các đường chéo chính AD, BE, CG bằng nhau và cắt nhau tạo O, tạo nên các tam giác đều ABO, BCO, CDO, DOE, GOE, AGO

Lại có trong tam giác đều, ta có ba cạnh bằng nhau, nên:

AB = OB = OA

BC = OB = OC 

CD = OD = OC 

OD = OE = DE 

OG = OE = GE 

AG = OG = OA

Vì vậy: OA = OB = OC = OD = OE = OG.