Giải 1.23 Toán 12 tập 1 SGK Kết nối tri thức

08:35:4301/10/2024

Lời giải bài 1.23 Toán 12 tập 1 SGK Kết nối tri thức được HayHocHoi trình bày chi tiết, ngắn gọn dễ hiểu nhất để học sinh lớp 12 tham khảo giải toán giỏi hơn.

Giải bài 1.23 Toán 12 tập 1 SGK Kết nối tri thức trang 32

Bài 1.23 Toán 12 Tập 1 Kết nối tri thức: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) $y=\frac{2x^2-x+4}{x-1}$

b) $y=\frac{x^2+2x+1}{x+3}$

Giải bài 1.23 Toán 12 Tập 1 Kết nối tri thức:

a) $y=\frac{2x^2-x+4}{x-1}$

• Tập xác định: D = R\{1}

• Sự biến thiên:

$y=\frac{2x^2-x+4}{x-1}=2x+1+\frac{5}{x-1}$

$y'=2-\frac{5}{(x-1)^2}=0$ $\Leftrightarrow x=\frac{2-\sqrt{10}}{2}$ hoặc $x=\frac{2+\sqrt{10}}{2}$

Trong khoảng $\left ( -\infty ;\frac{2-\sqrt{10}}{2} \right )$ và $\left ( \frac{2+\sqrt{10}}{2};+\infty \right )$ , y' > 0 nên hàm số đồng biến.

Trong khoảng $\dpi{100} \left ( \frac{2-\sqrt{10}}{2} ;1 \right )$ và $\left (1; \frac{2+\sqrt{10}}{2}\right )$ , y' < 0 nên hàm số nghịch biến.

• Cực trị:

Hàm số đạt cực đại tại $x=\frac{2-\sqrt{10}}{2}$ giá trị cực đại $y_{CD}=-2\sqrt{10}+3$

Hàm số đạt cực tiểu tại $x=\frac{2+\sqrt{10}}{2}$ giá trị cực tiểu $y_{CT}=2\sqrt{10}+3$

• Tiệm cận:

$\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }\frac{2x^2-x+4}{x-1}=-\infty$

$\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }\frac{2x^2-x+4}{x-1}=+\infty$

$\lim_{x\rightarrow 1^- }y=\lim_{x\rightarrow 1^- }\frac{2x^2-x+4}{x-1}=-\infty$

$\lim_{x\rightarrow 1^+ }y=\lim_{x\rightarrow 1^+}\frac{2x^2-x+4}{x-1}=+\infty$

Nên x = 1 là tiệm cận đứng của đồ thị hàm số

$\lim_{x\rightarrow -\infty }[y-(2x+1)]=\lim_{x\rightarrow -\infty }\left [2x+1+\frac{5}{x-1}-(2x+1) \right ]$ $= \lim_{x\rightarrow -\infty }\frac{5}{x-1}=0$

$\lim_{x\rightarrow +\infty }[y-(2x+1)]=\lim_{x\rightarrow +\infty }\left [2x+1+\frac{5}{x-1}-(2x+1) \right ]$ $= \lim_{x\rightarrow +\infty }\frac{5}{x-1}=0$

Nên y = 2x + 1 là tiệm cận xiên của đồ thị hàm số

• Bảng biến thiên:

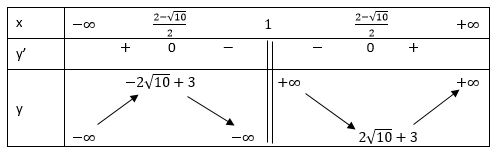
BBT câu a bài 1.23 trang 32 Toán 12 Tập 1 Kết nối tri thức

• Đồ thị

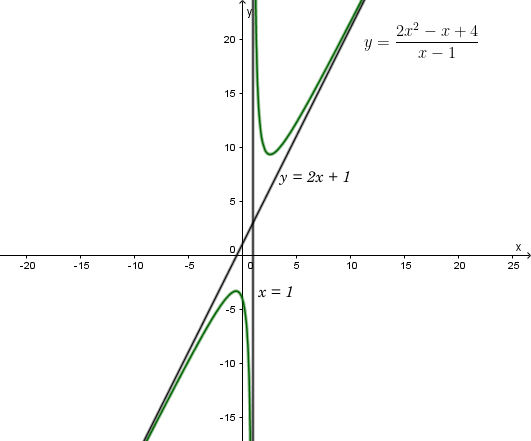
Đồ thị câu a bài 1.23 trang 32 Toán 12 Tập 1 Kết nối tri thức

Giao điểm của đồ thị hàm số với trục tung là (0; -4).

Đồ thị hàm số không cắt trục Ox.

Đồ thị hàm số nhận giao điểm I(1; 3) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.

b) $y=\frac{x^2+2x+1}{x+3}$

• Tập xác định: D = R\{-3}

• Sự biến thiên:

$y=\frac{x^2+2x+1}{x+3}=x-1+\frac{4}{x+3}$

$y'=1-\frac{4}{(x+3)^2}=0$ ⇔ x = -1 hoặc x = -5

Trong khoảng (-∞; - 5) và (-1; +∞), y' > 0 nên hàm số đồng biến.

Trong khoảng (-5; -3) và (-3; -1), y' < 0 nên hàm số nghịch biến.

• Cực trị:

Hàm số đạt cực đại tại x = -5 giá trị cực đại y_CĐ = -8

Hàm số đạt cực tiểu tại x= -1 giá trị cực tiểu y_CT = 0

• Tiệm cận:

$\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }\frac{x^2+2x+1}{x+3}=-\infty$

$\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }\frac{x^2+2x+1}{x+3}=+\infty$

$\lim_{x\rightarrow -3^- }y=\lim_{x\rightarrow -3^- }\frac{x^2+2x+1}{x+3}=-\infty$

$\lim_{x\rightarrow -3^+ }y=\lim_{x\rightarrow -3^+ }\frac{x^2+2x+1}{x+3}=+\infty$

Nên x = 3 là tiệm cận đứng của đồ thị hàm số

$\lim_{x\rightarrow -\infty }[y-(x-1)]=\lim_{x\rightarrow -\infty }\left [x-1+\frac{4}{x+1}-(x-1) \right ]$ $= \lim_{x\rightarrow -\infty }\frac{4}{x+3}=0$

$\lim_{x\rightarrow +\infty }[y-(x-1)]=\lim_{x\rightarrow +\infty }\left [x-1+\frac{4}{x+1}-(x-1) \right ]$ $= \lim_{x\rightarrow +\infty }\frac{4}{x+3}=0$

Nên y = x - 1 là tiệm cận xiên của đồ thị hàm số

• Bảng biến thiên:

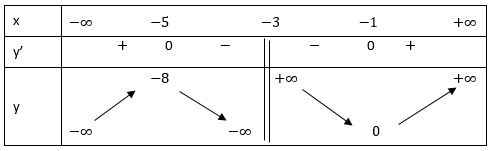
BBT câu b bài 1.23 trang 32 Toán 12 Tập 1 Kết nối tri thức

• Đồ thị

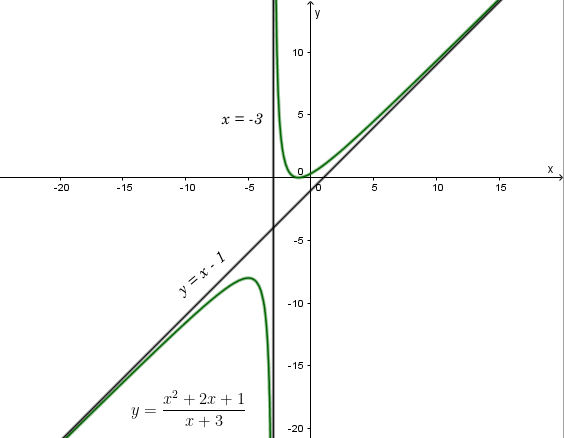
Đồ thị câu b bài 1.23 trang 32 Toán 12 Tập 1 Kết nối tri thức

Giao điểmcủa đồ thị hàm số với trục tung là (0; 1/3)

Giao điểm của đồ thị hàm số với trục hoành là điểm (-1; 0)

Đồ thị hàm số nhận giao điểm I(-3; -4) ủa hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.

Với nội dung giải bài 1.23 Toán 12 tập 1 Kết nối tri thức chi tiết, dễ hiểu ở trên. Hay Học Hỏi hy vọng giúp các em nắm vững phương pháp giải Toán 12 tập 1 Kết nối tri thức. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt.

» Xem thêm giải Toán 12 Tập 1 Kết nối tri thức SGK