Giải bài tập hệ phương trình, bất phương trình mũ và logarit cơ bản và nâng cao - Toán 12 chuyên đề

08:51:2209/12/2020

Các em đã làm quen cách giải phương trình mũ, bất phương trình mũ cũng như cách giải phương trình logarit và bất phương trình logarit ở các bài học trước đây.

Trong nội dung bài viết này, chúng ta sẽ giải một số bài tập về hệ phương trình, bất phương trình mũ và logarit từ cơ bản đến nâng cao.

Để giải được hệ phương trình hay bất phương trình mũ và logarit chúng ta cần kết hợp các phương pháp giải phương trình mũ và logarit với phương pháp giải hệ phương trình - bất phương trình đại số (chúng ta thường sử dụng phương pháp cộng hoặc phương pháp thế).

Các em có thể tham khảo bài viết về phương pháp giải phương trình và bất phương trình mũ cũng như cách giải phương trình và bất phương trình logarit đã được viết trên HayHocHoi.Vn.

I. Giải bài tập hệ phương trình, bất phương trình mũ và logarit

* Bài tập 1: Giải hệ phương trình mũ và logarit sau:

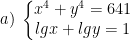
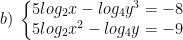
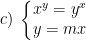
$a)\: \left\{\begin{matrix} x^4+y^4=641\\ lgx+lgy=1 \end{matrix}\right.$ $b)\: \left\{\begin{matrix} 5log_2x-log_4y^3=-8\\ 5log_2x^2-log_4y=-9 \end{matrix}\right.$ $c)\: \left\{\begin{matrix} x^y=y^x\\ y=mx \end{matrix}\right.$

* Lời giải:

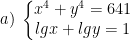
$a)\: \left\{\begin{matrix} x^4+y^4=641\\ lgx+lgy=1 \end{matrix}\right.$

- Điều kiện: x>0, y>0 hệ tương đương:

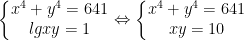
$\left\{\begin{matrix} x^4+y^4=641\\ lgxy=1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^4+y^4=641\\ xy=10 \end{matrix}\right.$

- Vì y>0, nên từ pt dưới của hệ ta được x = 10/y thay vào pt trên của hệ ta được:

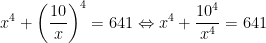
$x^4+\left (\frac{10}{x} \right )^4=641\Leftrightarrow x^4+\frac{10^4}{x^4}=641$

- Đặt x⁴ = t>0 ta được: 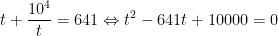$t+\frac{10^4}{t}=641\Leftrightarrow t^2-641t+10000=0$

Giải phương trình này được: t = 16 (nhận) hoặc t = 625 (nhận).

• TH1: t = 16 ⇒ x⁴ = 16 ⇒ x = 2 ⇒ y = 5;

• TH2: t = 625 ⇒ x⁴ = 625 ⇒ x = 5 ⇒ y = 2;

Vậy hệ phương trình có 2 cặp nghiệm của x và y là: (2;5) và (5;2)

* Nhận xét: Ta thấy hệ phương trình trên là hệ đối xứng, tức là vị trí x và y có thể đổi chỗ cho nhau nhưng không làm hệ phương trình thay đổi. Như vậy, với hệ phương trình đối xứng nếu có nghiệm sẽ có 2 cặp nghiệm của x và y.

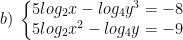
$b)\: \left\{\begin{matrix} 5log_2x-log_4y^3=-8\\ 5log_2x^2-log_4y=-9 \end{matrix}\right.$

- Điều kiện: x>0, y>0. Hệ tương đương:

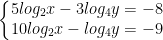
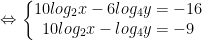
$\left\{\begin{matrix} 5log_2x-3log_4y=-8\\ 10log_2x-log_4y=-9 \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} 10log_2x-6log_4y=-16\\ 10log_2x-log_4y=-9 \end{matrix}\right.$

- Lấy phương trình ở trên trừ pt ở dưới của hệ ta được:

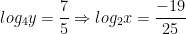
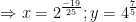
$log_4y=\frac{7}{5}\Rightarrow log_2x=\frac{-19}{25}$ $\Rightarrow x=2^{\frac{-19}{25}};y=4^{\frac{7}{5}}$

Vậy nghiệm của hệ trên là: 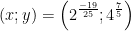$(x;y)=\left ( 2^{\frac{-19}{25}};4^{\frac{7}{5}} \right )$

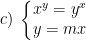
$c)\: \left\{\begin{matrix} x^y=y^x\\ y=mx \end{matrix}\right.$

- Điều kiện x>0, y>0.

- Nếu m = 1 thì y = x suy ra hệ có vô số nghiệm thỏa điều kiện x>0.

- Nếu m ≠ 1 và m > 0 ta có: 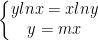$\left\{\begin{matrix} ylnx=xlny\\ y=mx \end{matrix}\right.$

- Do đó: mlnx = lny (*)

- Mặt khác: y = mx ⇒ lny = lnm + lnx (**)

- Từ (*) và (**) ta có: 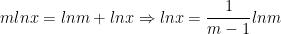$mlnx=lnm+lnx\Rightarrow lnx=\frac{1}{m-1}lnm$

Vậy hệ có nghiệm là: 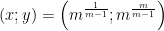$(x;y)=\left ( m^{\frac{1}{m-1}};m^{\frac{m}{m-1}} \right )$

⇒ Kết luận: Nếu m = 1 thì hệ có vô số nghiệm (x;y) = (a;a) với a>0.

Nếu m > 0 và m ≠ 1 hệ có cặp nghiệm 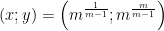$(x;y)=\left ( m^{\frac{1}{m-1}};m^{\frac{m}{m-1}} \right )$

* Bài tập 2: Giải hệ phương trình mũ và logarit sau:

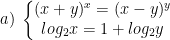
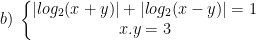
$a)\: \left\{\begin{matrix} (x+y)^x=(x-y)^y\\ log_2x=1+log_2y \end{matrix}\right.$ $b)\: \left\{\begin{matrix} \left |log_2(x+y) \right |+|log_2(x-y)|=1\\ x.y=3 \end{matrix}\right.$

* Lời giải:

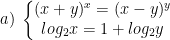
$a)\: \left\{\begin{matrix} (x+y)^x=(x-y)^y\\ log_2x=1+log_2y \end{matrix}\right.$

- Điều kiện: x,y>0

log₂x = 1 + log₂y ⇔ log₂x = log₂2 + log₂y ⇔ x = 2y.

(x + y)^x = (x - y)^y ⇔ (3y)^2y = y^y ⇔ (9y²)^y = y^y

⇔ 9y² = y ⇔ y(9y - 1) = 0 ⇔ y = 0 (loại) hoặc y = 1/9 (nhận).

Với y = 1/9 suy ra x = 2/9.

Vậy hệ có nghiệm là: x = 2/9; y = 1/9.

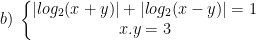
$b)\: \left\{\begin{matrix} \left |log_2(x+y) \right |+|log_2(x-y)|=1\\ x.y=3 \end{matrix}\right.$

- Ta có x.y = 3 ⇒ x,y cùng dấu (cùng âm hoặc cùng dương).

- Điều kiện x + y > 0 và x - y > 0 ⇒ x > 0 ⇒ y > 0.

Do đó, áp dụng BĐT Cauchy ta có:

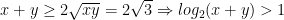
$x+y\geq 2\sqrt{xy}=2\sqrt{3}\Rightarrow log_2(x+y)>1$

Nên 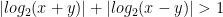$\left | log_2(x+y) \right |+\left | log_2(x-y) \right |>1$ ⇒ hệ vô nghiệm.

> Nhận xét: Ở câu b) ta dùng phương pháp đánh giá để dẫn đến kết luận hệ vô nghiệm.

* Bài tập 3: Giải hệ phương trình mũ và logarit sau:

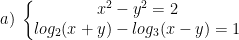
$a)\: \left\{\begin{matrix} x^2-y^2=2\\ log_2(x+y)-log_3(x-y)=1 \end{matrix}\right.$

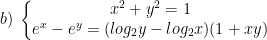
$b)\: \left\{\begin{matrix} x^2+y^2=1\\ e^x-e^y=(log_2y-log_2x)(1+xy) \end{matrix}\right.$

* Lời giải:

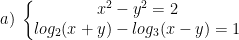
$a)\: \left\{\begin{matrix} x^2-y^2=2\\ log_2(x+y)-log_3(x-y)=1 \end{matrix}\right.$

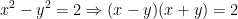
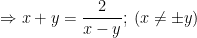
- Ta có: $x^2-y^2=2\Rightarrow (x-y)(x+y)=2$ $\Rightarrow x+y=\frac{2}{x-y};\: (x\neq \pm y)$

- Thay vào pt dưới: log₂(x + y) - log₃(x - y) = 1, ta được:

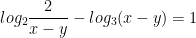
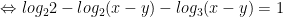
$log_2\frac{2}{x-y}-log_3(x-y)=1$ $\Leftrightarrow log_22-log_2(x-y)-log_3(x-y)=1$

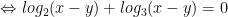
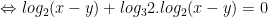
$\Leftrightarrow log_2(x-y)+log_3(x-y)=0$ $\Leftrightarrow log_2(x-y)+log_32.log_2(x-y)=0$

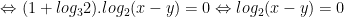
$\Leftrightarrow (1+log_32).log_2(x-y)=0\Leftrightarrow log_2(x-y)=0$

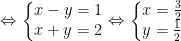
$\Leftrightarrow \left\{\begin{matrix} x-y=1\\ x+y=2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{3}{2}\\ y=\frac{1}{2} \end{matrix}\right.$

Vậy hệ có nghiệm x = 3/2; y = 1/2

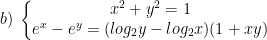
$b)\: \left\{\begin{matrix} x^2+y^2=1\\ e^x-e^y=(log_2y-log_2x)(1+xy) \end{matrix}\right.$

- Điều kiện: x,y>0

- Nếu x > y thì suy ra 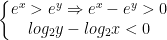$\left\{\begin{matrix} e^x>e^y\Rightarrow e^x-e^y>0\\ log_2y-log_2x<0 \end{matrix}\right.$

- Nếu x < y thì suy ra 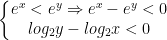$\left\{\begin{matrix} e^x<e^y\Rightarrow e^x-e^y<0\\ log_2y-log_2x<0 \end{matrix}\right.$

Do đó phương trình dưới của hệ không có nghiệm khi x ≠ y.

Với x = y thì 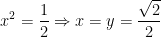$x^2=\frac{1}{2}\Rightarrow x=y=\frac{\sqrt{2}}{2}$

Vậy hệ phương trình có nghiệm 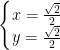$\left\{\begin{matrix} x=\frac{\sqrt{2}}{2}\\ y=\frac{\sqrt{2}}{2} \end{matrix}\right.$

* Bài tập 4: Giải hệ bất phương trình mũ và logarit sau:

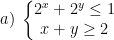
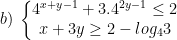
$a)\: \left\{\begin{matrix} 2^x+2^y\leq 1\\ x+y\geq 2 \end{matrix}\right.$ $b)\: \left\{\begin{matrix} 4^{x+y-1}+3.4^{2y-1}\leq 2\\ x+3y\geq 2-log_43 \end{matrix}\right.$

* Lời giải:

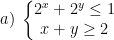
$a)\: \left\{\begin{matrix} 2^x+2^y\leq 1\\ x+y\geq 2 \end{matrix}\right.$

- Ta có: 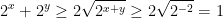$2^x+2^y\geq 2\sqrt{2^{x+y}}\geq 2\sqrt{2^{-2}}=1$

Do đó hệ có nghiệm khi: 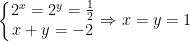$\left\{\begin{matrix} 2^x=2^y=\frac{1}{2}\\ x+y=-2 \end{matrix}\right.\Rightarrow x=y=1$

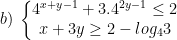
$b)\: \left\{\begin{matrix} 4^{x+y-1}+3.4^{2y-1}\leq 2\\ x+3y\geq 2-log_43 \end{matrix}\right.$

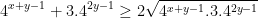
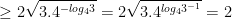
- Ta có: $4^{x+y-1}+3.4^{2y-1}\geq 2\sqrt{4^{x+y-1}.3.4^{2y-1}}$ $\geq 2\sqrt{3.4^{-log_43}}=2\sqrt{3.4^{log_43^{-1}}}=2$

hệ có nghiệm khi: 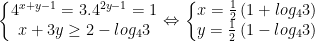$\left\{\begin{matrix} 4^{x+y-1}=3.4^{2y-1}=1\\ x+3y\geq 2-log_43 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{1}{2}\left ( 1+log_4 3\right )\\ y=\frac{1}{2}\left ( 1-log_43 \right ) \end{matrix}\right.$

> Nhận xét: Trong bài này vận dụng bất đẳng thức Cauchy cho 1 phương trình cua hệ, sau đó kết hợp với hệ còn lại để đưa ra kết luận nghiệm.

* Bài tập 5: Giải hệ bất phương trình mũ và logarit sau:

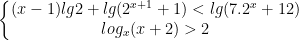
$\left\{\begin{matrix} (x-1)lg2+lg(2^{x+1}+1)<lg(7.2^x+12)\\ log_x(x+2)>2 \end{matrix}\right.$

* Lời giải:

- Xét phương trình: 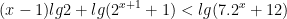$(x-1)lg2+lg(2^{x+1}+1)<lg(7.2^x+12)$

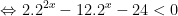
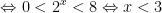$\Leftrightarrow 2.2^{2x}-12.2^x-24<0$ $\Leftrightarrow 0<2^x<8\Leftrightarrow x<3$ (*)

- Xét 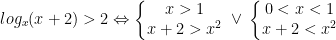$log_x(x+2)>2\Leftrightarrow \left\{\begin{matrix} x>1\\ x+2>x^2 \end{matrix}\right.\: \vee \: \left\{\begin{matrix} 0<x<1\\ x+2<x^2 \end{matrix}\right.$

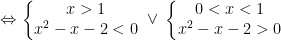
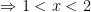$\Leftrightarrow \left\{\begin{matrix} x>1\\ x^2-x-2<0 \end{matrix}\right.\: \vee \: \left\{\begin{matrix} 0<x<1\\ x^2-x-2>0 \end{matrix}\right.$ $\Rightarrow 1<x<2$ (**)

Kết hợp (*) và (**) ta được hệ có nghiệm: 1<x<2.

II. Bài tập hệ phương trình, bất phương trình mũ nâng cao tự giải

* Bài tập 1: Giải hệ phương trình mũ và logarit sau:

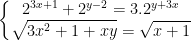
$\left\{\begin{matrix} 2^{3x+1}+2^{y-2}=3.2^{y+3x}\\ \sqrt{3x^2+1+xy}=\sqrt{x+1} \end{matrix}\right.$

* Đáp án Bài tập 1:

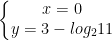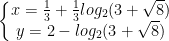
Hệ có nghiệm 2 cặp nghiệm là $\left\{\begin{matrix} x=0\\ y=3-log_211 \end{matrix}\right.$ và $\left\{\begin{matrix} x=\frac{1}{3}+\frac{1}{3}log_2(3+\sqrt{8})\\ y=2-log_2(3+\sqrt{8}) \end{matrix}\right.$

* Bài tập 2: Giải hệ phương trình mũ và logarit sau:

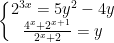
$\left\{\begin{matrix} 2^{3x}=5y^2-4y\\ \frac{4^x+2^{x+1}}{2^x+2}=y \end{matrix}\right.$

* Đáp án Bài tập 2:

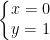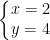
Hệ có nghiệm có 2 cặp nghiệm là $\left\{\begin{matrix} x=0\\ y=1 \end{matrix}\right.$ và $\left\{\begin{matrix} x=2\\ y=4 \end{matrix}\right.$

* Bài tập 3: Tìm m để hệ sau có 2 nghiệm phân biệt

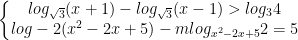
$\left\{\begin{matrix} log_{\sqrt{3}}(x+1)-log_{\sqrt{3}}(x-1)>log_34\\ log-2(x^2-2x+5)-mlog_{x^2-2x+5}2=5 \end{matrix}\right.$

* Đáp án Bài tập 3:

Để hệ có 2 nghiệm phân biệt thì m thỏa: 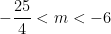$-\frac{25}{4}<m<-6$

* Bài tập 4: Tìm a để hệ sau có nghiệm ∀b ∈ R.

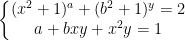
$\left\{\begin{matrix} (x^2+1)^a+(b^2+1)^y=2\\ a+bxy+x^2y=1 \end{matrix}\right.$

* Đáp án Bài tập 4:

Với a = 1 thì hệ có nghiệm ∀b ∈ R.

* Bài tập 5: Cho hệ phương trình mũ sau:

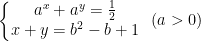
$\left\{\begin{matrix} a^x+a^y=\frac{1}{2}\\ x+y=b^2-b+1 \end{matrix}\right.\: \: (a>0)$

i) Giải hệ khi b = 1

ii) Tìm a để hệ có nghiệm ∀b ∈ [0;1].

* Đáp án Bài tập 5:

i) Với b = 1. hệ có 2 cặp nghiệm :

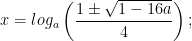
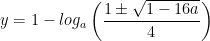
$x=log_a\left ( \frac{1\pm \sqrt{1-16a}}{4} \right );$ $y=1-log_a\left ( \frac{1\pm \sqrt{1-16a}}{4} \right )$

ii) Khi $0<a\leq \frac{1}{32\sqrt[3]{2}}$ hệ có nghiệm ∀b ∈ [0;1]

Như vậy các em thấy việc vận dụng các kiến thức đã biết về hệ phương trình, phương trình, bất phương trình mũ và logarit cần sự biến đổi linh hoạt và huy động nhiều kiến thức các em đã học trước đó. Các em cần làm nhiều bài tập để rèn được kỹ năng giải các bài toán này. Hy vọng với việc giải bài tập về hệ phương trình, bất phương trình mũ và logarit ở trên hữu ích cho các em, chúc các em học tập tốt.

Giải bài tập hệ phương trình, bất phương trình mũ và logarit cơ bản và nâng cao - Toán 12 chuyên đề

Tags:

Đánh giá & nhận xét