Giải phương trình Mũ và Logarit bằng phương pháp hàm số - Toán 12 chuyên đề
Để giải phương trình mũ và logarit chúng ta có 3 phương pháp, phổ biến nhất là đưa về cùng cơ số và đặt ẩn phụ kế đến là logarit hóa hai vế, còn giải phương trình mũ và logarit bằng phương pháp hàm số ít được sử dụng hơn.
Tuy nhiên, phương pháp giải phương trình mũ và logarit bằng hàm số đối với một số bài toán mang lại hiệu quả rất bất ngờ. Cách giải phương trình mũ bằng phương pháp hàm số như thế nào? chúng ta cùng tham khảo bài viết dưới đây.
» Đừng bỏ lỡ: Dựa vào đồ thị biện luận theo m số nghiệm của phương trình cực hay
° Hàm số - kiến thức cần nhớ
• Tính chất 1: Nếu hàm f(x) tăng (hoặc giảm) trong khoảng (a;b) thì phương trình f(x) = k có không quá một nghiệm trong khoảng (a;b).
• Tính chất 2: Nếu hàm f(x) tăng trong khoảng (a;b) và hàm g(x) là hàm hằng hoặc là một hàm giảm trong khoảng (a;b) thì phương trình f(x) có nhiều nhất một nghiệm thuộc khoảng (a;b), (do đó nếu tồn tại x0 ∈ (a;b): f(x0) = g(x0) thì đó là nghiệm duy nhất của phương trình f(x) = g(x)).
° Giải phương trình mũ và logarit bằng phương pháp hàm số ta thực hiện các bước sau:
• Bước 1: Chuyển phương trình về dạng f(x) = k.
• Bước 2: Xét hàm số y = f(x).
Dùng lập luận khẳng định hàm số đơn điệu (đồng biến hoặc nghịch biến).
• Bước 3: Nhận xét:
- Với x = x0 ⇔ f(x) = f(x0) = k, do đó x = x0 là nghiệm.
- Với x > x0 ⇔ f(x) > f(x0) ⇔ f(x) > k, nên phương trình vô nghiệm.
- Với x < x0 ⇔ f(x) < f(x0) ⇔ f(x) < k, nên phương trình vô nghiệm.
• Bước 4: Kết luận: x = x0 là nghiệm duy nhất của phương trình.
° Bài tập vận dụng giải phương trình mũ và logarit bằng phương pháp hàm số
* Bài tập 1: Giải các phương trình mũ và logarit sau:
a) 2x + 5x = 7
b) log3(x+3) + log5(x+5) = 2
* Lời giải:
- Với bài tập này thì vế trái làm hàm mũ hoặc logarit, vế phải là hàm hằng.
a) 2x + 5x = 7
- Ta có: VT = 2x + 5x , là hàm đồng biến
VP = 7, là một hàm hằng.
→ Như vậy, nếu phương trình có nghiệm thì nghiệm đó là duy nhất.
- Mặt khác, ta thấy: với x = 1 thì:
VT = 21 + 51 = 7 = VP
⇒ Phương trình có nghiệm duy nhất x = 1.
b) log3(x+3) + log5(x+5) = 2
- Điều kiện: x ≥ -3.
- Ta có: VT = log3(x+3) + log5(x+5) là một hàm đồng biến
VP = 2 là hàm hằng
→ Như vậy, nếu phương trình có nghiệm thì nghiệm đó là duy nhất.
- Mặt khác, ta thấy: với x = 0 (thỏa điều kiện x ≥ -3) thì:
VT =log3(3) + log5(5) = 1 + 1 = 2 = VP
⇒ Phương trình có nghiệm duy nhất x = 0.
* Bài tập 2: Giải các phương trình sau.
a) 5x = 6 - x
b) log6x = 7 - x.
* Lời giải:
- Với bài tập này thì vế trái làm hàm mũ hoặc logarit, vế phải là hàm số bậc 1.
a) 5x = 6 - x
- Ta có: VT = 5x , là hàm đồng biến
VP = 6 - x, là một hàm nghịch biến.
→ Như vậy, nếu phương trình có nghiệm thì nghiệm đó là duy nhất.
- Mặt khác, ta thấy: với x = 1 thì:
VT = 51 = 5; VP = 6 - 1 = 5 ⇒ VT = VP
⇒ Phương trình có nghiệm duy nhất x = 1.
b) log6x = 7 - x.
- Ta có: VT = log6x , là hàm đồng biến
VP = 7 - x, là một hàm nghịch biến.
→ Như vậy, nếu phương trình có nghiệm thì nghiệm đó là duy nhất.
- Mặt khác, ta thấy: với x = 6 thì:
VT = log66 = 1; VP = 7 - 6 = 1 ⇒ VT = VP
⇒ Phương trình có nghiệm duy nhất x = 6.
* Bài tập 3: Giải pương trình: log2x + log5(2x+1) = 2.
* Lời giải:
- Điều kiện logarit có nghĩa: x >0
- Ta có: VT = log2x + log5(2x+1) , là hàm đồng biến.
VP = 2 là hàm hằng.
→ Như vậy, nếu phương trình có nghiệm thì nghiệm đó là duy nhất.
- Mặt khác, ta thấy: với x = 2 thì:
VT = log22 + log5(2.2+1) = 1 + 1 = 2 = VP.
⇒ Phương trình có nghiệm duy nhất x = 2.
• Cũng có thể lập luận như sau:
- Nhận thấy x = 2 là nghiệm.
+ Nếu x > 2 thì:
log2x > log22 = 1; log5(2x + 1) > log2(2.2 + 1) = 1.
⇒ log2x + log5(2x+1) > 2
⇒ Phương trình vô nghiệm.
+ Nếu 0<x<2 thì:
log2x < log22 = 1; log5(2x + 1) < log2(2.2 + 1) = 1.
⇒ log2x + log5(2x+1) < 2
⇒ Phương trình vô nghiệm.
→ Kết luận: Phương trình có nghiệm duy nhất x = 2.
* Bài tập 4: Giải phương trình: 31-x - log2x - 1 = 0
* Lời giải:
- Điều kiện log có nghĩa: x > 0
- Ta có: 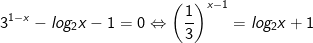
- Ta thấy:
VT = (1/3)x-1 : của phương trình là một hàm nghịch biến.
VP = log2x + 1: của phương trình là một hàm đồng biến.
→ Vì vậy, nếu phương trình có nghiệm thì nghiệm đó là duy nhất.
- Mặt khác, ta nhẩm thấy x = 1 là nghiệm của phương trình vì:
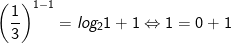
⇒ Phương trình có nghiệm duy nhất x = 1.
* Bài tập 5: Giải phương trình: 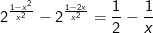 (*)
(*)
* Lời giải:
- Điều kiện: x≠0
- Nhận thấy:
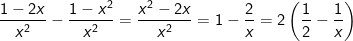
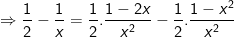
- Do đó phương trình (*) tương đương với phương trình:
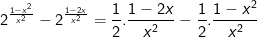
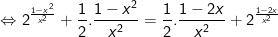
- Mặt khác: 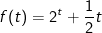 là hàm số đồng biến trên R, do đó để:
là hàm số đồng biến trên R, do đó để:
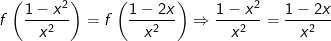
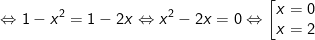
- Đối chiếu điều kiện x = 0 (loại), x = 2 (nhận).
⇒ Phương trình (*) có nghiệm duy nhất x = 2.
* Bài tập tự làm (vận dụng giải phương trình mũ và logarit phương pháp bằng hàm số)
* Bài tập 1: Giải phương trình mũ sau: 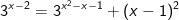
* Bài tập 2: Giải phương trình mũ sau: 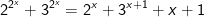
* Bài tập 2: Giải phương trình sau: 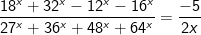
Như vậy, chúng ta thấy rằng đối với một số bài toán về hàm số mũ và hàm số logarit khi giải bằng phương pháp hàm số sẽ đi đến kết quả nhanh hơn, hiệu quả hơn so với các phương pháp khác. Phương pháp này thường vận dụng với các bài toán dễ nhẩm được nghiệm.
Hy vọng với bài viết về Giải phương trình Mũ và Logarit bằng phương pháp hàm số của Hay Học Hỏi ở trên giúp ích cho các em. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để ghi nhận và hỗ trợ, chúc các em học tốt.
Đánh giá & nhận xét
-
 Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ
Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ
-
 Bài 1 trang 82 Toán 12 tập 1 Cánh Diều
Bài 1 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 8 trang 81 Toán 12 tập 1 Cánh Diều
Bài 8 trang 81 Toán 12 tập 1 Cánh Diều
-
 Bài 7 trang 81 Toán 12 tập 1 Cánh Diều
Bài 7 trang 81 Toán 12 tập 1 Cánh Diều
-
 Bài 6 trang 81 Toán 12 tập 1 Cánh Diều
Bài 6 trang 81 Toán 12 tập 1 Cánh Diều
-
 Bài 5 trang 81 Toán 12 tập 1 Cánh Diều
Bài 5 trang 81 Toán 12 tập 1 Cánh Diều
-
 Bài 4 trang 80 Toán 12 tập 1 Cánh Diều
Bài 4 trang 80 Toán 12 tập 1 Cánh Diều
-
 Bài 3 trang 80 Toán 12 tập 1 Cánh Diều: Phép Toán Vectơ
Bài 3 trang 80 Toán 12 tập 1 Cánh Diều: Phép Toán Vectơ
-
 Bài 2 trang 80 Toán 12 tập 1 Cánh Diều
Bài 2 trang 80 Toán 12 tập 1 Cánh Diều
-
 Bài 1 trang 80 Toán 12 tập 1 Cánh Diều
Bài 1 trang 80 Toán 12 tập 1 Cánh Diều
-
 Bài 9 trang 73 Toán 12 tập 1 Cánh Diều
Bài 9 trang 73 Toán 12 tập 1 Cánh Diều
-
 Bài 8 trang 73 Toán 12 tập 1 Cánh Diều
Bài 8 trang 73 Toán 12 tập 1 Cánh Diều
-
 Bài 7 trang 73 Toán 12 tập 1 Cánh Diều
Bài 7 trang 73 Toán 12 tập 1 Cánh Diều
-
 Bài 6 trang 73 Toán 12 tập 1 Cánh Diều
Bài 6 trang 73 Toán 12 tập 1 Cánh Diều
-
 Bài 5 trang 73 Toán 12 tập 1 Cánh Diều
Bài 5 trang 73 Toán 12 tập 1 Cánh Diều
-
 Bài 4 trang 72 Toán 12 tập 1 Cánh Diều
Bài 4 trang 72 Toán 12 tập 1 Cánh Diều
-
 Bài 3 trang 72 Toán 12 tập 1 Cánh Diều
Bài 3 trang 72 Toán 12 tập 1 Cánh Diều
-
 Bài 2 trang 72 Toán 12 tập 1 Cánh Diều
Bài 2 trang 72 Toán 12 tập 1 Cánh Diều
-
 Bài 1 trang 72 Toán 12 tập 1 Cánh Diều
Bài 1 trang 72 Toán 12 tập 1 Cánh Diều
-
 Bài 5 trang 64 Toán 12 tập 1 Cánh Diều
Bài 5 trang 64 Toán 12 tập 1 Cánh Diều
-
 Bài 4 trang 64 Toán 12 tập 1 Cánh Diều
Bài 4 trang 64 Toán 12 tập 1 Cánh Diều
-
 Bài 3 trang 63 Toán 12 tập 1 Cánh Diều
Bài 3 trang 63 Toán 12 tập 1 Cánh Diều
-
 Bài 2 trang 63 Toán 12 tập 1 Cánh Diều
Bài 2 trang 63 Toán 12 tập 1 Cánh Diều
-
 Bài 1 trang 63 Toán 12 tập 1 Cánh Diều
Bài 1 trang 63 Toán 12 tập 1 Cánh Diều
-
 Bài 14 trang 48 Toán 12 tập 1 Cánh Diều
Bài 14 trang 48 Toán 12 tập 1 Cánh Diều
-
 Bài 13 trang 48 Toán 12 tập 1 Cánh Diều
Bài 13 trang 48 Toán 12 tập 1 Cánh Diều






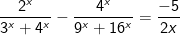
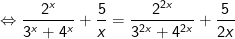
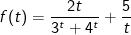 luôn đồng biến nên f(t1) = f(t2) thì t1 = t2.
luôn đồng biến nên f(t1) = f(t2) thì t1 = t2.











































