Giải bài 2 trang 104 Toán 8 Tập 1 SGK Cánh Diều

Bài 2 trang 104 Toán 8 Tập 1 Cánh Diều:

Người ta ghép ba hình tam giác đều có độ dài cạnh là a với vị trí như Hình 31.

a) Chứng minh ba điểm A, B, C thẳng hàng.

b) Chứng minh tứ giác ACDE là hình thang cân.

c) Tính diện tích của tứ giác ACDE theo a.  

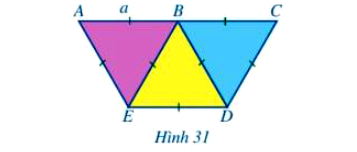
Giải bài 2 trang 104 Toán 8 Tập 1 Cánh Diều:

a) Vì ΔABE, ΔBED, ΔBDC là các tam giác đều nên:

Vì vậy:

⇒ 3 điểm A, B, C thẳng hàng.

b) Vì ΔABE, ΔBED là các tam giác đều nên:

Mà hai góc này ở vị trí so le trong nên AC // ED

Tứ giác ACDE có AC // ED nên là hình thang.

Mặt khác, ta có:

 (do ΔABE, ΔBDC là các tam giác đều)

⇒ Hình thang ACDE là hình thang cân.

c) Vẽ đường cao EH của ΔAEB như sau:

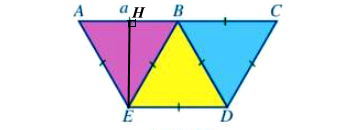
Vì ΔAEB là tam giác đều nên H là trung điểm của AB, nên:

Xét ΔEHB vuông tại H, theo định lí Pythagore ta có:

EB² = EH² + HB²

⇒ EH² = EB² – HB²

Ta có AC = AB + BC = a + a = 2a.

Diện tích hình thang cân ACDE là:

  (đvdt)