Lý thuyết Toán 7 Bài 1: Tập Hợp Các Số Hữu Tỉ - Ví Dụ chi tiết (Kết Nối Tri Thức)
Chào mừng các em học sinh đến với Bài 1: Tập hợp các số hữu tỉ trong chương trình Toán 7 sách Kết nối tri thức. Bài học này là nền tảng để các em làm quen với một tập hợp số mới, mở rộng từ tập hợp số nguyên đã học.
1. Khái Niệm Số Hữu Tỉ và Biểu Diễn Trên Trục Số
-
Khái niệm: Số hữu tỉ là số viết được dưới dạng phân số
với
và
.
Tập hợp các số hữu tỉ được ký hiệu là
.
-
Cách biểu diễn số hữu tỉ
trên trục số:
-
Chia đoạn thẳng đơn vị thành
bphần bằng nhau, lấy một đoạn làm đơn vị mới. -
Điểm biểu diễn số hữu tỉ
cách gốc
Omột đoạn bằngađơn vị mới. Điểm này nằm sau gốcOnếu số hữu tỉ dương và nằm trước gốcOnếu số hữu tỉ âm.
-
Ví dụ:
-
Các số
là các số hữu tỉ vì chúng có thể viết dưới dạng phân số:
,
,
.
-
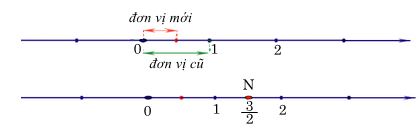
Để biểu diễn số hữu tỉ
trên trục số, ta chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Điểm biểu diễn là điểm
Nnằm sau gốcOvà cáchOmột đoạn bằng 3 đơn vị mới.
-
Số đối: Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ
mlà số hữu tỉ-m. Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với gốcOvà có cùng khoảng cách đếnO.
 Số đối của số hữu tỉ
Số đối của số hữu tỉ là số hữu tỉ
được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.
2. Thứ Tự Trong Tập Hợp Các Số Hữu Tỉ
-
So sánh: Ta có thể so sánh hai số hữu tỉ bất kỳ bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.
-
Tính chất:
-
Với hai số hữu tỉ
a, bbất kỳ, ta luôn cóa = bhoặca < bhoặca > b. -
Tính chất bắc cầu: Cho ba số hữu tỉ
a, b, c. Nếua < bvàb < cthìa < c.
-
-
Biểu diễn trên trục số: Nếu
a < bthì điểmanằm trước điểmbtrên trục số.
Ví dụ:
-
So sánh
0,5và: Ta có
.
Vì
nên
.
-
So sánh
và
: Vì
và
, theo tính chất bắc cầu, ta có
.
-
Lưu ý:
-
Trên trục số, các điểm nằm trước gốc
Obiểu diễn số hữu tỉ âm (< 0). -
Các điểm nằm sau gốc
Obiểu diễn số hữu tỉ dương (> 0). -
Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
-
Bài viết trên đã cung cấp cho các em những kiến thức cơ bản về tập hợp các số hữu tỉ. Nắm vững các khái niệm và tính chất này sẽ là nền tảng vững chắc để học tốt các bài tiếp theo.
• Xem thêm:
Lý thuyết Toán 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ
Lý thuyết Toán 7 Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ
Lý thuyết Toán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế
Đánh giá & nhận xét
-
 Lý thuyết Toán 7 Bài 6: Số Vô Tỉ & Căn Bậc Hai Số Học (Kết Nối Tri Thức)
Lý thuyết Toán 7 Bài 6: Số Vô Tỉ & Căn Bậc Hai Số Học (Kết Nối Tri Thức)
-
 Lý thuyết Toán 7 Bài 7: Tập Hợp Các Số Thực - Lý Thuyết và Bài Tập (Kết Nối Tri Thức)
Lý thuyết Toán 7 Bài 7: Tập Hợp Các Số Thực - Lý Thuyết và Bài Tập (Kết Nối Tri Thức)
-
 Lý thuyết Toán 7 Bài 5: Số Thập Phân Vô Hạn Tuần Hoàn (Kết Nối Tri Thức)
Lý thuyết Toán 7 Bài 5: Số Thập Phân Vô Hạn Tuần Hoàn (Kết Nối Tri Thức)
-
 Lý Thuyết Toán 7 Bài 4: Thứ Tự Thực Hiện Các Phép Tính, Quy Tắc Chuyển Vế
Lý Thuyết Toán 7 Bài 4: Thứ Tự Thực Hiện Các Phép Tính, Quy Tắc Chuyển Vế
-
 Lý thuyết Toán 7 Bài 3: Lũy Thừa Với Số Mũ Tự Nhiên (Kết Nối Tri Thức)
Lý thuyết Toán 7 Bài 3: Lũy Thừa Với Số Mũ Tự Nhiên (Kết Nối Tri Thức)
-
 Lý thuyết Toán 7 Bài 2: Cộng, Trừ, Nhân, Chia Số Hữu Tỉ (Kết Nối Tri Thức)
Lý thuyết Toán 7 Bài 2: Cộng, Trừ, Nhân, Chia Số Hữu Tỉ (Kết Nối Tri Thức)
-
 Mục lục SGK Toán 7 tập 1 Kết nối tri thức - Lý thuyết và bài tập Toán 7 tập 1 Kết nối tri thức
Mục lục SGK Toán 7 tập 1 Kết nối tri thức - Lý thuyết và bài tập Toán 7 tập 1 Kết nối tri thức


















































