Các dạng bài tập về thể tích khối đa diện (khối chóp, khối lăng trụ) - Toán hình 12 chuyên đề
Thể tích của một khối đa diện hiểu theo nghĩa thông thường là số đo độ lớn phần không gian mà nó chiếm chỗ. Từ xa xưa con người đã tìm cách đo thể tích của các khối vật chất trong tự nhiên.
Đối với những vật thể lỏng như khối nước trong một cái bể chứa, người ta có thể dùng những cái thùng có kích thước nhỏ hơn để đong. Đối với những vật rắn có kích thước nhỏ người ta có thể thả chúng vào một cái thùng đổ đầy nước rồi đo lượng nước trào ra,...
Tuy nhiên, trong thực tế không có nhiều vật thể không thể đo được thể tích bằng những cách trên. Vì vậy, người ta tìm cách thiết lập những công thức tính thể tích của một số khối đa diện đơn giản khi biết kích thước của chúng và từ đó tìm cách tính thể tích của các khối đa diện phức tạp hơn.
Ở bài viết này, chúng ta sẽ cùng làm hệ thống lại các dạng bài tập về tính thể tích của khối đa diện (khối chóp, lăng trụ và một số khối đa diện khác) và làm các ví dụ minh họa để biết cách vận dụng linh hoạt công thức trong các bài toán khác nhau.
I. Công thức tính thể tích khối đa diện
1. Công thức tính thể tích khối chóp
• Thể tích khối chóp: 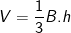
B: Diện tích mặt đáy (đa giác đáy).
h: Độ dài đường cao
2. Công thức tính thể tích khối lăng trụ
• Thể tích khối lăng trụ: 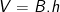
B: Diện tích mặt đáy (đa giác đáy).
h: Độ dài đường cao
3. Công thức tính thể tích hình hộp chữ nhật
• Thể tích hình hộp chữ nhật: 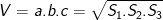
a; b; c là độ dài các cạnh (dài, rộng, cao) của hình hộp chữ nhật.
• Công thức tính độ dài đường chéo của hình hộp chữ nhật: 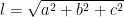
4. Công thức tính thể tích khối lập phương
• Thể tích khối lập phương: 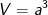
a là độ dài cạnh của khối lập phương.
• Công thức tính độ dài đường chéo của khối lập phương: 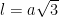
5. Công thức tính thể tích khối chóp cụt
• Thể tích khối chóp cụt: 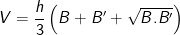
Trong đó: B, B' là diện tích hai đáy,
h là chiều cao khối chóp cụt.
6. Công thức tính thể tích hình cầu (khối cầu)
• Thể tích hình cầu (khối cầu): 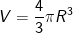
• Diện tích mặt cầu: 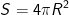
Trong đó: R là bán kính khối cầu (mặt cầu, hình cầu).
7. Công thức tính thể tích hình trụ (khối trụ)
• Thể tích hình trụ (khối trụ): 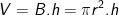
• Diện tích xung quanh hình trụ: 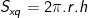
• Diện tích toàn phần hình trụ (bằng diện tích xung quanh và diện tích 2 mặt đáy): 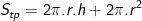
Trong đó: B là diện tích đáy
h là chiều cao; r là bán kính đáy
> Lưu ý: Với hình trụ thì chiều cao bằng độ dài đường sinh (h = l) nên ở các công thức tính diện tích xung quanh và diện tích toàn phần dùng h.
8. Công thức tính thể tích hình nón (khối nón)
• Thể tích hình nón (khối nón): 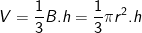
• Diện tích xung quanh hình nón: 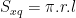
• Diện tích toàn phần hình nón: 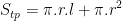
Trong đó: B là diện tích đáy
h là chiều cao; r là bán kinh đáy; l là dộ dài đường sinh
II. Các dạng bài tập tính thể tích khối đa diện (khối chóp, khối lăng trụ)
* Phương pháp giải chung:
+ Bài toán cơ bản ta có thể áp dụng trực tiếp các công thức tính thể tích của khối đa diện
+ Bài toán khó hơn thì ta cần chia khối đa diện thành các khối nhỏ hơn, mà thể tích của các khối nhỏ này có thể tính bằng công thức và phần bù vào cũng tính được thể tích.
1. Dạng bài tập tính thể tích khối chóp
* Ở dạng này có một số bài tập như:
+ Tính thể tích của khối chóp có cạnh bên vuông góc với đáy
+ Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy
+ Tính thể tích khối chóp có mặt bên vuông góc với đáy
+ Tính tỉ số thể tích của 2 khối chóp
* Ví dụ 1 (Bài 1 trang 25 SGK Hình học 12): Tính thể tích khối tứ diện đều cạnh a.
* Lời giải:
- Tứ diện đều cạnh a minh họa như hình sau: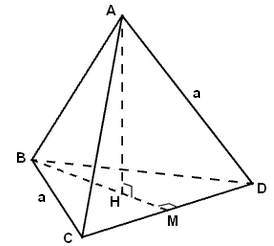
- Gọi ABCD là tứ diện đều cạnh a; H là tâm đường tròn ngoại tiếp tam giác BCD
⇒ HB = HC = HD nên H nằm trên trục đường tròn ngoại tiếp tam giác BCD. (1)
- Lại có: AB = AC = AD vì ABCD là tứ diện đều
⇒ HA là trục đường tròn ngoại tiếp tam giác BCD
⇒ HA ⊥ (BCD)
- Vì ΔBCD là tam giác đều nên H là trọng tâm ΔBCD.
- Gọi M là trung điểm của CD, xét tam giác BCD ta có:
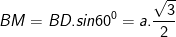
- Lại có: 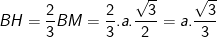
- Áp dụng định lí pytago vào tam giác vuông AHB ta được:
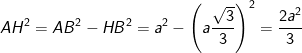
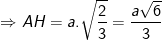
- Ta có diện tích tam giác đều BCD cạnh a là:
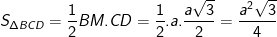
- Vậy thể tích khối tứ diện đều ABCD là:
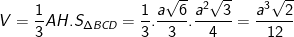
* Ví dụ 2 (Bài 3 trang 25 SGK Hình học 12): Cho khối hộp ABCD.A'B'C'D'. Tính tỉ số giữa thể tích của khối hộp đó và thể tích của khối tứ diện ACB'D'.
* Lời giải:
- Minh họa khối hộp như hình vẽ
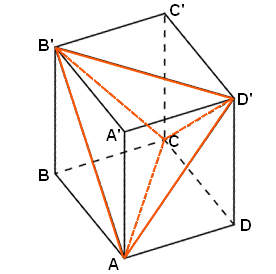
- Gọi S là diện tích đáy và h là chiều cao của khối hộp, khi đó thể tích của khối hộp là: V = S.h
- Chia khối hộp thành tứ diện thàn ACB'D' (các cạnh của tứ diện là các đường chéo) và bốn khối chóp A.A'B'D'; C.C'B'D'; B'.BAC; D'.DAC; (khối chóp có các cạnh bên là các cạnh hình hộp, các cạnh đáy là các đường chéo).
- Xét khối chóp A.A'B'D' có diện tích đáy là S/2 và chiều cao là h, nên thể tích của khối chóp này là:
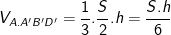
- Tương tự như vậy thì thể tích các khối chóp còn lại:
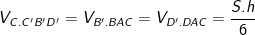
- Vậy thể tích của tứ diện là:
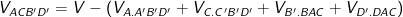
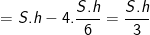
- Vậy tỉ số thể tích của khối hộp và tứ diện là: 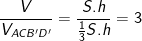
* Ví dụ 3 (Bài 5 trang 26 SGK Hình học 12): Cho tam giác ABC, vuông cân ở A và AB = a. Trên đường thẳng qua C, vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với BD cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a.
* Lời giải:
- Minh họa như hình vẽ sau: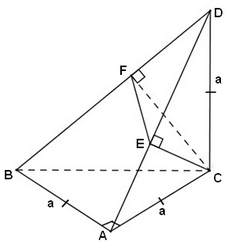
- Ta có: BA ⊥ CD và BA ⊥ CA nên suy ra BA ⊥ (ADC) ⇒ BA ⊥ CE
- Mặt khác BD ⊥ (CEF) ⇒ BD ⊥ CE
- Từ đó suy ra: CE ⊥ (ABD) ⇒ CE ⊥ EF và CE ⊥ AD
Vì ΔACD vông cân do AC = CD = a; nên
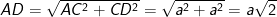
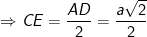
- Ta có: 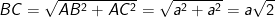
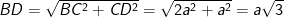
- Áp dụng hệ thức lượng trong tam giác vuông BCD ta có:
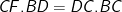
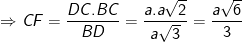
- Từ đó suy ra:
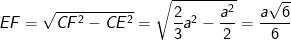
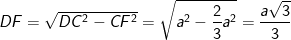
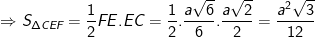
- Vậy 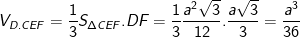
* Ví dụ 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B, AC=a√2, SA vuông góc với mặt phẳng (ABC), SA = a. Tính thể tích khối chóp S.ABC
* Lời giải:
- Minh họa hình chóp như hình vẽ sau:
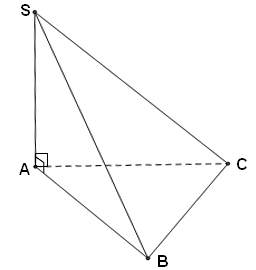 - ABC là tam giác vuông cân ở B, AC=a√2 nên ta có:
- ABC là tam giác vuông cân ở B, AC=a√2 nên ta có:
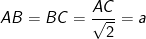
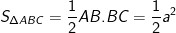
- Vì SA vuông góc với mặt phẳng ABC nên SA là đường cao, ta có:
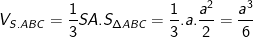
* Ví dụ 5: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AD = 2a, AB = a. Gọi H là trung điểm AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA=a√5.
* Lời giải:
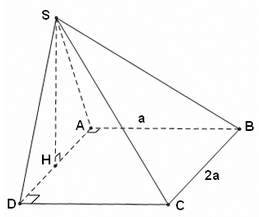
- Ta có: 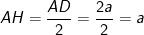
- Độ dài đường cao hình chóp: 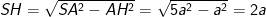
- Vậy thể tích của hình chóp là: 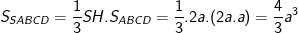
2. Dạng bài tập tính thể tích khối lăng trụ
* Ở dạng này có một số bài tập như:
+ Tính thể tích của khối lăng trụ đứng, lăng trụ đều
+ Tính thể tích của khối lăng trụ xiên
* Ví dụ 1 (Bài 4 trang 26 SGK Hình học 12): Cho hình lăng trụ và hình chóp có diện tích đáy và chiều cao bằng nhau. Tính tỉ số thể tích của chúng.
* Lời giải:
- Minh họa lăng trụ như hình sau: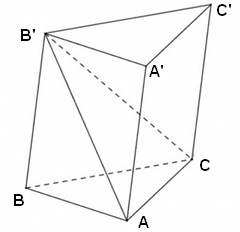
- Gọi S là diện tích đáy và h là chiều cao của hình lăng trụ và của hình chóp, ta có:
- Thể tích khối lăng trụ là:
- Thể tích khối chóp là: 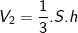

* Ví dụ 2: Cho hình hộp đứng có các cạnh AB = 3a, AD = 2a, AA'= 2a. Tính thể tích của khối A'.ACD'.
* Lời giải:
- Minh họa như hình vẽ sau: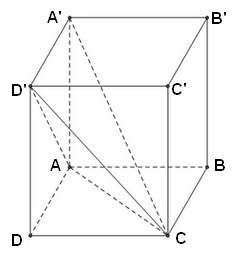
- Do mặt bên ADD'A' là hình chữ nhật nên ta có:
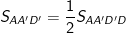
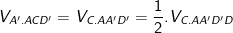

* Ví dụ 3: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a√3, góc giữa (A'CA) và đáy là 60º. Gọi M là trung điểm của BB'. Tính thể tích của khối chóp M.A'B'C'.
* Lời giải:
- Minh họa lăng trụ như hình vẽ: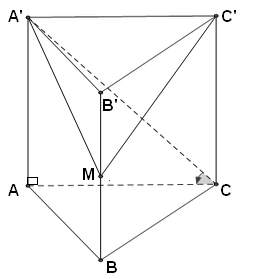
- Vì AA' ⊥ (ABC) nên suy ra: 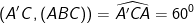
- Ta có: 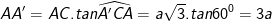
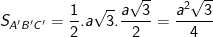 (đường cao trong tam giác đều cạnh a có độ dài là a√3/2).
(đường cao trong tam giác đều cạnh a có độ dài là a√3/2).
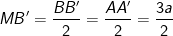
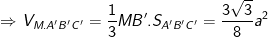
Như vậy, mấu chốt cơ bản để giải bài toán tính thể tích của khối đa diện (khối chóp, khối lăng trụ) là các em phải nhớ được công thức. Từ giả thiết bài toán các em cần xác định được chiều cao của chóp hay lăng trụ, và tính được diện tích đáy của chóp (hay lăng trụ).
Hy vọng qua bài viết trên, các em đã hiểu rõ, ghi nhớ và vận dụng được các công thức và cách tính thể tích của khối đa điện một cách linh hoạt trong mỗi bài toán cụ thể. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để ghi nhận và hỗ trợ, chúc các em học tốt.
Đánh giá & nhận xét
-
 Bài 7 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 7 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 6 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 6 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 5 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 5 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 4 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 4 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 3 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 3 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 2 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 2 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 1 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 1 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ
Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ


















































