Giải Toán 10 trang 9 tập 2 Kết nối tri thức

Luyện tập 3 Toán 10 trang 9 Tập 2 Kết nối tri thức:

Vẽ đồ thị của các hàm số y = 3x + 1 và y = – 2x². Hãy cho biết:

a) Hàm số y = 3x + 1 đồng biến hay nghịch biến trên R. 

b) Hàm số y = – 2x² đồng biến hay nghịch biến trên mỗi khoảng: (– ∞; 0) và (0; + ∞).

Giải Luyện tập 3 Toán 10 trang 9 Tập 2 Kết nối tri thức:

* Hàm số y = 3x + 1

Tập xác định của hàm số là R. 

Với x = 0 thì y = 1, với x = – 1 thì y = – 2 nên đồ thị hàm số y = 3x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; – 2). 

* Hàm số y = –2x²

Tập xác định của hàm số là R. 

Bảng giá trị tương ứng của x và y 

Trên mặt phẳng tọa độ, lấy các điểm (0; 0), (1; – 2), (– 1; – 2), (2; – 8), (– 2; – 8) rồi lần lượt nối chúng để được đường cong là đồ thị của hàm số y = – 2x². 

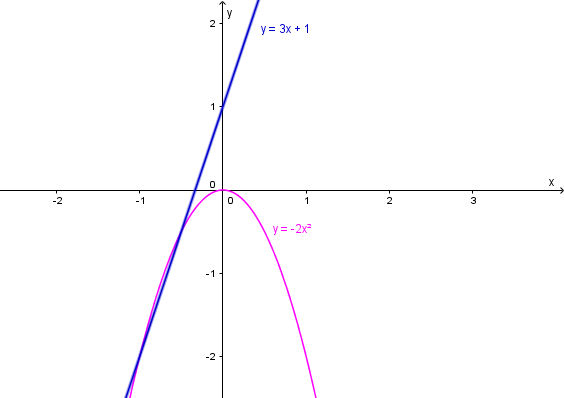
a) Quan sát hình trên, ta thấy đồ thị hàm số y = 3x + 1 đi lên từ trái sang phải trên nên hàm số y = 3x + 1 đồng biến trên . 

b) Quan sát hình trên ta thấy:

+ Trên khoảng (–∞; 0), đồ thị hàm số y = –2x²đi lên từ trái sang phải nên hàm số đồng biến trên khoảng này. 

+ Trên khoảng (0; +∞), đồ thị hàm số y = –2x² đi xuống từ trái sang phải nên hàm số nghịch biến trên khoảng này. 

Vận dụng Toán 10 trang 9 Tập 2 Kết nối tri thức:

Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.

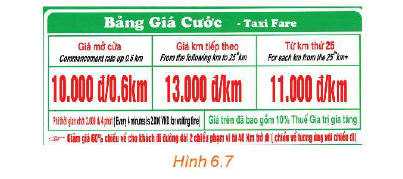
a) Tính số tiền phải trả khi di chuyển 25 km.

b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.

c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.

Giải vận dụng Toán 10 trang 9 Tập 2 Kết nối tri thức:

a) Khi di chuyển 25 km thì khách hàng phải trả 10 000 đồng cho 0,6 km đầu (giá mở cửa) và 13 000 đồng trên 1 km cho 25 – 0,6 = 24,4 km sau (giá tính cho km tiếp theo dưới 25 km). 

Do đó tổng số tiền phải trả khi di chuyển 25 km là: 

10 000 + 24,4 . 13 000 = 327 200 (đồng). 

Vậy số tiền phải trả khi di chuyển 25 km là 327 200 đồng. 

b) Gọi x (km, x > 0) là độ dài quãng đường di chuyển và y (đồng) là số tiền phải trả tương ứng. 

Ta có: 

+ Giá mở cửa là 10 000 đồng cho 0,6 km đầu, tức là khi x ≤ 0,6 thì số tiền phải trả tương ứng là y = 10 000. 

+ Giá tiền cho km tiếp theo dưới 25 km là 13 000 đồng trên 1 km, tức là khi 0,6 < x < 25 thì số tiền phải tương ứng là y = 10 000 + 13 000(x – 0,6) hay y = 13 000x + 2 200.

+ Giá tiền phải trả cho km thứ 25 trở lên là 11 000 đồng trên 1 km, tức là khi x ≥ 25 thì số tiền phải trả tương ứng là y = 10 000 + 13 000 . 24,4 + 11 000(x – 25) hay y = 11 000 x + 52 200. 

Vậy ta có công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển là: 

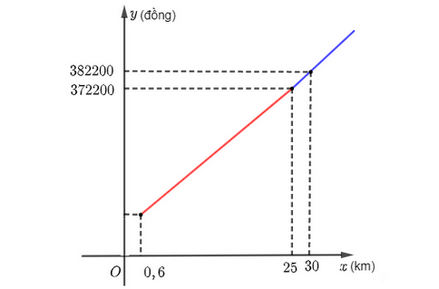
c) Ta vẽ đồ thị hàm số: 

cách vẽ các đồ thị y = 10 000 trên (0; 0,6], đồ thị y = 13 000x + 2 200 trên (0,6; 25) và đồ thị y = 11 000x + 52 200 trên [25; + ∞). 

Đồ thị hàm số có dạng như sau: 

Bài 6.1 trang 9 Toán 10 Tập 2 Kết nối tri thức:

Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x?

a) x + y = 1; 

b) y = x²; 

c) y²= x; 

d) x² – y² = 0. 

> Giải bài 6.1 trang 9 Toán 10 Tập 2 Kết nối tri thức

Bài 6.2 trang 9 Toán 10 Tập 2 Kết nối tri thức:

Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó. 

> Giải bài 6.2 trang 9 Toán 10 Tập 2 Kết nối tri thức

Bài 6.3 trang 9 Toán 10 Tập 2 Kết nối tri thức:

Tìm tập xác định của các hàm số sau: 

a) y = 2x³ + 3x + 1;

b)

c) 

> Giải bài 6.3 trang 9 Toán 10 Tập 2 Kết nối tri thức

Bài 6.4 trang 9 Toán 10 Tập 2 Kết nối tri thức:

Tìm tập xác định và tập giá trị của mỗi hàm số sau: 

a) y = 2x + 3; 

b) y = 2x².

> Giải bài 6.4 trang 9 Toán 10 Tập 2 Kết nối tri thức

Bài 6.5 trang 9 Toán 10 Tập 2 Kết nối tri thức:

Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng. 

a) y = – 2x + 1; 

b) 

> Giải bài 6.5 trang 9 Toán 10 Tập 2 Kết nối tri thức

Bài 6.6 trang 9 Toán 10 Tập 2 Kết nối tri thức:

Giá thuê xe ô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và 900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe. 

a) Viết công thức của hàm số T = T(x). 

b) Tính T(2), T(3), T(5) và cho biết ý nghĩa của mỗi giá trị này. 

> Giải bài 6.6 trang 9 Toán 10 Tập 2 Kết nối tri thức