Đồ thị hàm số bậc nhất y=ax+b, cách vẽ, hệ số góc của đường thẳng? Ví dụ? Toán 8 bài 4 [b4c3cd1]

Đồ thị hàm số y=ax+b là đường thẳng, cách vẽ đồ thị hàm số bậc nhất y = ax như nào? hệ số góc của đường thẳng là gì? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0)

• Định nghĩa đồ thị hàm số bậc nhất :

Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng.

* Chú ý:

- Đồ thị của hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b (a ≠ 0).

- Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b.

* Ví dụ: Dưới đây là đồ thị hàm số bậc nhất

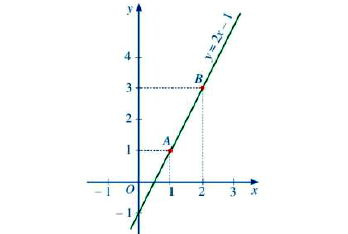
2. Cách vẽ đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0)

• Cách vẽ đồ thị hàm số y = ax (a ≠ 0)

Để vẽ đồ thị của hàm số y = ax (a ≠ 0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.

* Ví dụ: Vẽ đồ thị của hàm số y = −2x.

* Lời giải:

Với x = 1 thì y = −2, ta được A(1; −2) thuộc đồ thị hàm số y = −2x.

Vậy đồ thị của hàm số y = −2x là đường thẳng đi qua hai điểm O(0; 0) và A(1; −2).

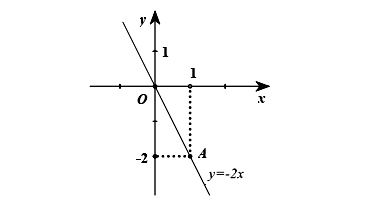
• Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0; b ≠ 0)

Để vẽ đồ thị của hàm số y = ax + b (a ≠ 0; b≠ 0), ta có thể xác định hai điểm P(0; b) và Q  rồi vẽ đường thẳng đi qua hai điểm đó.

* Ví dụ: Vẽ đồ thị của hàm số y = −2x + 2.

* Lời giải:

Với x = 0 thì y = 2, ta được điểm P(0; 2) thuộc đồ thị của hàm số y = −2x + 2.

Với y = 0 thì x = 1, ta được điểm Q(1; 0) thuộc đồ thị của hàm số y = −2x + 2.

Vẽ đồ thị của hàm số y = −2x + 2 là đường thẳng đi qua hai điểm P(0; 2), Q(1; 0).

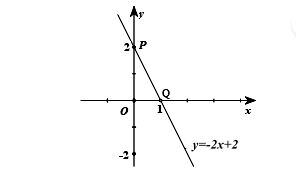
3. Hệ số góc của đường thẳng

a) Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox

Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox. T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.

Góc α tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc α).

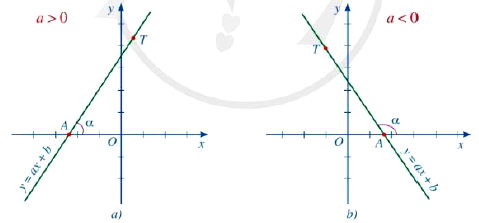
b) Hệ số góc

• Định nghĩa: Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠ 0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a ≠ 0).

* Chú ý:

- Khi hệ số a > 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.

- Khi hệ số a < 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.

* Ví dụ: Hệ số góc của đường thẳng y = 2x + 1 là 2.

Hệ số góc của đường thẳng y = −5x + 11 là −5.

c) Ứng dụng của hệ số góc

Cách nhận biết vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy:

Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0).

a) Nếu d song song với d’ thì a = a’; b ≠ b’. Ngược lại, nếu a = a’; b ≠ b’ thì d song song với d’.

b) Nếu d trùng với d’ thì a = a’; b = b’. Ngược lại, nếu a = a’; b = b’ thì d trùng với d’.

c) Nếu d và d’ cắt nhau thì a ≠ a’. Ngược lại, nếu a ≠ a’ thì d và d’ cắt nhau.

* Ví dụ: 

- Hai đường thẳng y = 2x + 1; y = 2x + 3 có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng này song song.

- Hai đường thẳng y = 2x + 1; y = 3x có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.

- Hai đường thẳng y = 3x – 1; y = 3x −1 có hệ số góc và hệ số tự do giống nhau nên hai đường thẳng này trùng nhau.