Công thức tính xác suất thực nghiệm, khả năng xảy ra của 1 sự kiện? Toán 6 chân trời Tập 2 chương 9 Bài 2

Khái niệm khả năng xảy ra của 1 sự kiện, Công thức tính xác suất thực nghiệm như nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Khả năng xảy ra của một sự kiện 

• Khi thực hiện một phép thử nghiệm, một sự kiện có thể xảy ra hoặc không thể xảy ra. Để nói về khả năng xảy ra của mỗi sự kiện, ta dùng một con số có giá trị từ 0 đến 1.

• Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.

• Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.

* Ví dụ: Trong hộp có 5 quả bóng xanh và 1 quả bóng đỏ. Không nhìn vào hộp, chọn ra từ hộp một quả bóng. Xét các sự kiện sau:

- Bóng chọn ra có màu vàng;

- Bóng chọn ra không có màu vàng.

- Bóng chọn ra có màu xanh.

Sự kiện nào có khả năng xảy ra cao nhất?

* Lời giải:

- Sự kiện “Bóng chọn ra có màu vàng” không thể xảy ra. Vì trong hộp không có quả bóng màu vàng.

- Sự kiện “Bóng chọn ra không có màu vàng:” chắc chắn xảy ra. Vì trong hộp không có quả bóng màu vàng.

- Trong hộp có cả quả bóng màu xanh và màu đỏ. Khi lấy ra một quả bóng từ trong hộp ra thì có thể lấy được số quả bóng màu xanh hoặc màu đỏ.

Do đó, sự kiện “Bóng chọn ra có màu xanh” có thể xảy ra.

Vậy sự kiện có khả năng xảy ra cao nhất là: “Bóng chọn ra không có màu vàng”.

2. Xác suất thực nghiệm 

• Thực hiện lặp đi lặp lại một hoạt động nào đó n lần. Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số

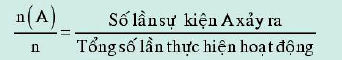
được gọi là xác suất thực nghiệm của sự kiện A sau n hoạt động vừa thực hiện.

* Ví dụ: Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:

a) Sơn phải chờ xe dưới 1 phút.

b) Sơn phải chờ xe từ 5 phút trở lên.

* Lời giải:

Tổng số lần Sơn chờ xe buýt là: 4 + 10 + 4 + 2 = 20 (lần).

a) Số lần Sơn phải chờ xe dưới 1 phút là 4 (lần).

Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 1 phút” là: 

Vậy xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 1 phút” là 1/5.

b) Số lần Sơn phải chờ xe từ 5 phút trở lên là tổng số lần Sơn chờ xe từ 5 phút đến 10 phút và từ 10 phút trở lên.

Do đó, số lần Sơn phải chờ xe từ 5 phút trở lên là: 4 + 2 = 6 (lần).

Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là: 

Vậy xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là 3/10 .