Khái niệm Giá trị tuyệt đối của một số thực, tính chất của giá trị tuyệt đối? Toán 7 bài 3 cd1c2

Khái niệm Giá trị tuyệt đối của một số thực là gì, tính chất của giá trị tuyệt đối như nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Khái niệm giá trị tuyệt đối của một số thực

- Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu |x|.

* Nhận xét:

- Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x.

- Hai số thực đối nhau có giá trị tuyệt đối bằng nhau.

* Ví dụ: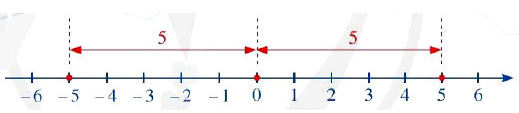 

- Khoảng cách từ điểm 5 đến gốc 0 là 5 nên giá trị tuyệt đối của số 5 là 5, tức là |5| = 5.

- Khoảng cách từ điểm –5 đến gốc 0 là 5 nên giá trị tuyệt đối của số –5 là 5, tức là |–5| = 5.

- Số 5 và –5 là hai số đối nhau, |5| = |–5| = 5.

2. Tính chất giá trị tuyệt đối của một số thực

- Nếu x là số dương thì giá trị tuyệt đối của x là chính nó: |x| = x (x > 0).

- Nếu x là số âm thì giá trị tuyệt đối của x là số đối của nó: |x| = – x (x < 0).

- Giá trị tuyệt đối của 0 là 0: |0| = 0.

* Nhận xét: Với mỗi số thực x, ta có:

• 

• |– x| = |x|.

* Ví dụ 1: Tìm: |–79|; |10,7|; ; 

* Lời giải:

Ta có:

|–79| = –(–79) = 79.

|10,7| = 10,7

* Ví dụ 2: Cho x = –12. Tính giá trị của mỗi biểu thức sau: 

a) 18 + |x|;

b) 25 – |x|; 

c) |3 + x | – |7|.

* Lời giải:

a) Với x = –12 ta có |x| = |–12| = –(–12) = 12.

Khi đó ta có: 18 + |x| = 18 + 12 = 30.

b) Với x = –12 ta có |x| = |–12| = –(–12) = 12.

Khi đó ta có: 25 – |x| = 25 – 12 = 13.

c) Thay x = –12 vào biểu thức ta được: 

|3 + (–12)| – |7| = |–9| – |7| = –(–9) – 7 = 9 – 7 = 2.

* Chú ý: Giả sử hai điểm A, B lần lượt biểu diễn hai số thực a, b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a – b|, tức là AB = |a – b|.

* Ví dụ 3: Trên trục số, tính độ dài đoạn thẳng AB trong mỗi trường hợp sau:

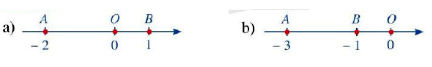
* Lời giải:

a) Ta có: AB = OA + OB = |–2| + |1| = 2 + 1 = 3

b) Ta có: AB = OA – OB = |–3| – |–1| = 3 – 1 = 2