Cách biểu diễn số thực trên trục số, so sánh hai số thực, số đối của một số thực? Toán 7 bài 2 cd1c2

Cách biểu diễn số thực trên trục số, so sánh hai số thực, số đối của một số thực? câu trả lời sẽ có ngay trong nội dung bài viết này.

I. Tập hợp số thực

1. Số thực

- Số hữu tỉ và số vô tỉ được gọi chung là số thực.

- Tập hợp các số thực được kí hiệu là ℝ.

* Ví dụ: Các số: 1,5;  là các số thực

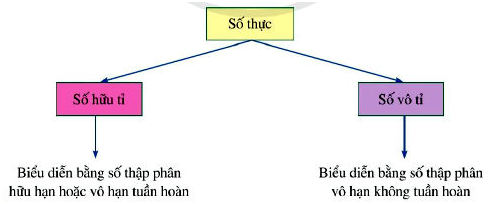
2. Biểu diễn thập phân của số thực

- Mỗi số thực là số hữu tỉ hoặc số vô tỉ. Vì thế, mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn. Ta có sơ đồ sau:

II. Biểu diễn số thực trên trục số

Tương tự như đối với số hữu tỉ, ta có thể biểu diễn mọi số thực trên trục số, khi đó điểm biểu diễn số thực x được gọi là điểm x.

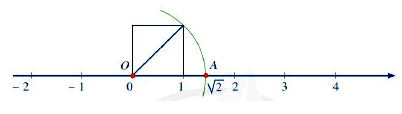
* Ví dụ: Biểu diễn số thực  trên trục số: 

* Lời giải:

Số  là một số vô tỉ vì vậy để biểu diễn số  trên trục số ta làm như sau:

- Vẽ một hình vuông với một cạnh là đoạn thẳng có hai đầu mút là điểm gốc 0 và điểm 1. Khi đó, đường chéo của hình vuông có độ dài cạnh bằng 

- Vẽ một phần đường tròn tâm là điểm gốc 0, bán kính là , cắt trục số tại điểm A nằm bên phải gốc 0. Ta có OA = và A là điểm biểu diễn .

* Nhận xét:

- Không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

- Mỗi số thực được biểu diễn bởi một điểm trên trục số; Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

Vậy trục số còn được gọi là trục số thực.

III. Số đối của một số thực

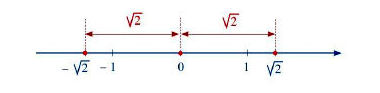
- Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau.

- Số đối của số thực a kí hiệu là – a.

- Số đối của số 0 là 0.

* Nhận xét: Số đối của – a là số a, tức là –(–a) = a.

* Ví dụ: Số đối của số thực  là số thực 

IV. So sánh hai số thực

1. So sánh hai số thực

Cũng như số hữu tỉ, trong hai số thực khác nhau luôn có một số nhỏ hơn số kia.

- Nếu số thực a nhỏ hơn số thực b thì ta biết a < b hay b > a.

- Số thực lớn hơn 0 gọi là số thực dương.

- Số thực nhỏ hơn 0 gọi là số thực âm.

- Số 0 không phải là số thực dương cũng không phải số thực âm.

- Nếu a < b và b < c thì a < c.

2. Cách so sánh hai số thực

- Ta có thể so sánh hai số thực bằng cách biểu diễn thập phân mỗi số thực đó rồi so sánh hai số thập phân đó.

- Việc biểu diễn một số thực dưới dạng số thập phân (hữu hạn hoặc vô hạn) thường là phức tạp. Trong một số trường hợp ta dùng quy tắc: Với a, b là hai số thực dương, nếu: a > b thì 

* Ví dụ: So sánh các số thực sau:

a) –1,(27) và –1,272 ;

b)  và 

* Lời giải:

a) Ta viết –1,(27) = –1,27272727... sau đó ta so sánh với –1,272.

Hai số –1,27272727… và –1,2720 có phần nguyên và đến hàng phần nghìn giống nhau, cặp chữ số khác nhau đầu tiên bắt đầu từ hàng phần chục nghìn.

Do 7 > 0 nên 1,27272727...> 1,2720, suy ra –1,27272727... < –1,2720.

Vậy –1,(27) < –1,272.

b) Ta có: 0 < 7 < 8 nên  < 

3. Minh hoạ trên trục số

Giả sử hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số nằm ngang. Ta có nhận xét sau :

- Nếu x < y hay y > x thì điểm x nằm bên trái điểm y;

- Ngược lại nếu điểm x nằm bên trái điểm y thì x < y hay y > x.

Đối với hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số thẳng đứng, ta cũng có nhận xét sau :

- Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y;

- Ngược lại, nếu điểm x nằm phía dưới điểm y thì x < y hay y > x.

* Ví dụ: a) Sắp xếp các số sau theo thứ tự tăng dần: 3; –1; 

b) Trong ba điểm A, B, C trên trục số dưới đây có một điểm biểu diễn số thực . Hãy xác định điểm đó.

* Lời giải:

a) Ta có: –1 , 0 và 0 <  nên –1 < 

Do 2 < 9 nên  <  mà  = 3 nên  < 3

Vậy các số đã cho được sắp xếp thứ tự tăng dần là: –1; ; 3.

b) Do –1 <  < 3 nên điểm  năm bên phải điểm –1 và nằm bên trái điểm 3 trên trục số nằm ngang. Nên trong ba điểm A, B, C chỉ có điểm B thoả mãn hai điều kiện đó.
Vậy điểm B biểu diễn số thực