Công thức tính diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, tứ giác? Toán 7 bài 2 cd1c3

Công thức tính diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, tứ giác như thế nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Hình lăng trụ đứng tam giác

- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.

- Hai mặt đáy cùng là tam giác và song song với nhau; Mỗi mặt bên là hình chữ nhật;

- Các cạnh bên bằng nhau;

- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.

* Ví dụ: Hình lăng trụ đứng tam giác ABC.A'B'C' có:

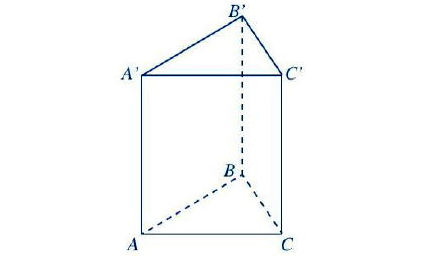
- Đáy dưới là tam giác ABC, đáy trên là tam giác A'B'C';

Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'A'A;

- Các cạnh:

+ Cạnh đáy: AB, BC, CA, A'B', B'C', C'A'

+ Cạnh bên: AA', BB', CC';

- Các đỉnh: A, B, C, A', B', C'.

- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC'.

2. Hình lăng trụ đứng tứ giác

- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.

- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.

- Các cạnh bên bằng nhau.

- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.

* Ví dụ: Hình lăng trụ đứng tứ giác ABCD.A'B'C'D' có:

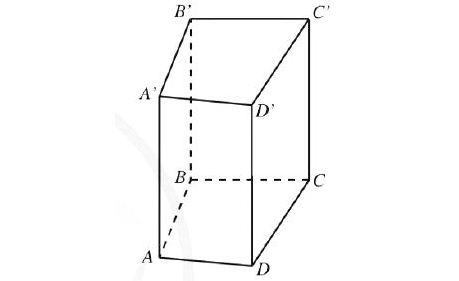
- Đáy dưới là tứ giác ABCD, đáy trên là tứ giác A'B'C'D';

Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'D'D, DD'A'A;

- Các cạnh:

+ Cạnh đáy: AB, BC, CD, DA, A'B', B'C', C'D', D'A'

+ Các cạnh bên: AA', BB', CC', DD' bằng nhau.

- Các đỉnh: A, B, C, D, A', B', C', D'.

- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC' hoặc DD'.

* Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.

3. Công thức tính thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

• Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.

→ Công thức tính thể tích hình lăng trụ đứng tức giác là: : V = S . h,

Trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.

• Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.

→ Công thức tính thể tích hình lăng trụ đứng tam giác là: V = S . h

Trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.

• Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.

→ Công thức tính diện tích xung quanh của lăng trụ dứng tam giác và lăng trụ đứng tứ giác là: S_xq = C . h

Trong đó S_xq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.

* Ví dụ: a) Cho hình lăng trụ đứng tam giác ABC.A'B'C'.

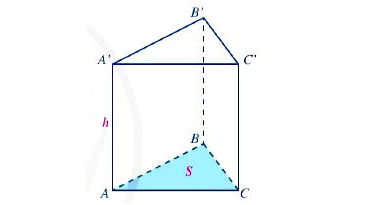
S_xq = C . h, trong đó C là chu vi của tam giác ABC (hoặc tam giác A'B'C'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC').

V = S . h, trong đó S là diện tích tam giác ABC (hoặc A'B'C'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC').

b) Cho hình lăng trụ đứng tứ giác ABCD.A'B'C'D':

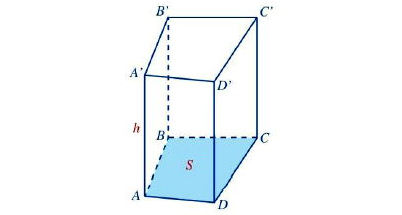
S_xq = C . h, trong đó C là chu vi của tứ giác ABCD (hoặc tứ giác A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC', hoặc DD').

V = S . h, trong đó S là diện tích tứ giác ABCD (hoặc A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC', hoặc DD').