Bài 9 trang 96 Toán 10 tập 2 Kết nối tri thức

Bài 9 trang 96 Toán 10 Tập 2 Kết nối tri thức:

Cho hàm số y = f(x) = ax² + bx + c với đồ thị là parabol (P) có đỉnh I(5/2; -1/4) và đi qua điểm A(1; 2).

a) Biết rằng phương trình của parabol có thể viết dưới dạng y = a(x – h)² + k, trong đó I(h, k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.

b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

c) Giải bất phương trình f(x) ≥ 0.

Phân Tích Hướng Dẫn Giải:

1. Tìm phương trình (a): Sử dụng dạng đỉnh $y = a(x-h)^2 + k$ với $h=5/2, k=-1/4$. Thay tọa độ điểm $A(1; 2)$ để tìm hệ số $a$. Sau đó tìm các giao điểm với trục tọa độ để vẽ.

2. Đồng biến/Nghịch biến (b): Dựa vào đỉnh $I$ và hệ số $a$ (bề lõm) để xác định.

3. Giải BPT (c): Dựa vào đồ thị (hoặc dùng Đại số) để tìm các giá trị $x$ mà đồ thị nằm trên hoặc chạm trục hoành ($f(x) \ge 0$).

Giải bài 9 trang 96 Toán 10 Tập 2 Kết nối tri thức:

a) Vì parabol có đỉnh I(5/2; -1/4) nên ta có h = 5/2 và k = -1/4. Suy ra phương trình của parabol (P) có dạng: $y=a\left ( x-\frac{5}{2} \right )^2-\frac{1}{4}$

Vì parabol (P) đi qua điểm A(1; 2) nên ta có:

$2=a\left ( 1-\frac{5}{2} \right )^2-\frac{1}{4}\Rightarrow a=1$

Vậy parabol (P) có phương trình là: $y=1.\left ( x-\frac{5}{2} \right )^2-\frac{1}{4}$

hay y = x² – 5x + 6.

* Vẽ parabol (P): 

Parabol có đỉnh $I\left ( \frac{5}{2};-\frac{1}{4} \right )$, hệ số a = 1> 0 nên parabol có bề lõm hướng lên trên.

Phương trình trục đối xứng: x = 5/2

Giao điểm của (P) với trục tung có tọa độ là B(0; 6). 

Phương trình x² – 5x + 6 = 0 có hai nghiệm x = 2 và x = 3. Vậy giao điểm của (P) với trục hoành là C(2; 0) và D(3; 0). 

Vẽ đường cong đi qua các điểm trên ta được parabol (P).

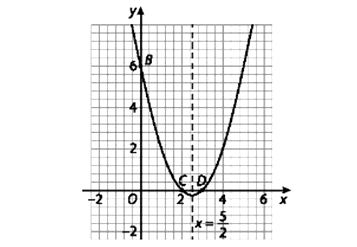
b) Từ parabol (P) đã vẽ ở câu a, ta có hàm số y = x² – 5x + 6 đồng biến trên khoảng $\left ( \frac{5}{2};+\infty \right )$ và nghịch biến trên khoảng $ \left (-\infty; \frac{5}{2} \right )$

c) Ta có: f(x) ≥ 0 

⇔ x² – 5x + 6 ≥ 0

⇔ x ≤ 2 hoặc x ≥ 3 (từ đồ thị suy ra)

Vậy tập nghiệm của bất phương trình là S = (–∞; 2] ∪ [3; +∞).