Đường trung trực của một đoạn thẳng khái niệm, tính chất và vận dụng? Toán 7 chân trời tập 2 chương 8 bài 5

Đường trung trực của một đoạn thẳng khái niệm, tính chất và vận dụng như nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Đường trung trực của một đoạn thẳng

• Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đó.

* Ví dụ: Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N, P và trên cạnh DC lấy các điểm M’, N’, P’. Cho biết AM = MN = NP = PB và MM’, NN’, PP’ đều song song với BC (Hình 3).

Tìm đường trung trực của mỗi đoạn thẳng AB, AN và NB.

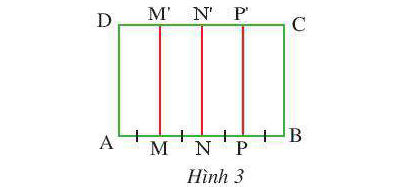
* Lời giải:

Do ABCD là hình chữ nhật nên MM’ ⊥ AB, NN’ ⊥ AB, PP’ ⊥ AB.

Ta có AN = AM + MN; NB = NP + PB.

Do AM = MN = NP = PB nên AN = NB và N nằm giữa AB do đó N là trung điểm của AB.

Khi đó NN’ ⊥ AB và N là trung điểm của AB nên đường trung trực của đoạn AB là NN’.

2. Tính chất của đường trung trực

• Định lí 1: Điểm nằm trên trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

* Ví dụ: Trong hình vẽ dưới đây có d là đường thẳng trung trực của đoạn thẳng AB. Với điểm M ∈ d thì ta suy ra được MA = MB.

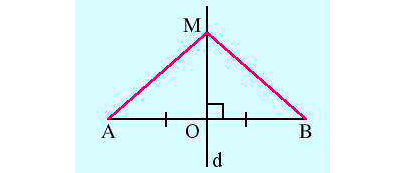
• Định lí 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

* Ví dụ 1: Trong hình vẽ dưới đây có d là đường trung trực của đoạn thẳng AB.

Ta có: MA = MB suy ra điểm M thuộc đường thẳng d.

* Ví dụ 2: Trong Hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x.

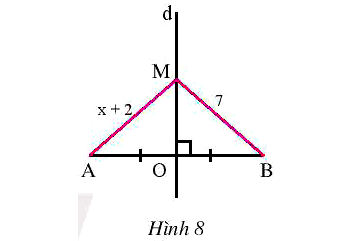* Lời giải:

Vì M thuộc đường trung trực của đoạn thẳng AB nên MA = MB.

Do đó x + 2 = 7 ⇒ x = 5.

3. Cách vẽ đường trung trực của đoạn thẳng

Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:

- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn AB (Hình 9a).

- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b).

- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN.

* Chú ý: 

- Khi vẽ hai cung tròn trên, ta phải lấy bán kính lớn hơn AB thì hai cung tròn đó mới có hai điểm chung.

- Giải điểm của đường thẳng MN với đoạn thẳng AB là trung điểm của đoạn thẳng AB nên cách vẽ trên cũng là cách dựng trung điểm của đoạn thẳng bằng thước và compa.